【题目】设![]() 为等差数列
为等差数列![]() 的前n项和,
的前n项和,![]() 是正项等比数列,且
是正项等比数列,且![]() ,
,![]() .在①
.在①![]() ,②
,②![]() ,③
,③![]() 这三个条件中任选一个,回答下列为题:
这三个条件中任选一个,回答下列为题:
(1)求数列![]() 和
和![]() 的通项公式;
的通项公式;
(2)如果![]() (m,
(m,![]() ),写出m,n的关系式
),写出m,n的关系式![]() ,并求
,并求![]() .
.
参考答案:
【答案】(1)见解析;(2)![]() ;
;![]()
【解析】
(1)若选①②,结合等差数列与等比数列通项公式的基本量计算,即可求得公差和公比,即可求得数列![]() 和
和![]() 的通项公式;若选③,结合等差数列前n项和公式、等差数列与等比数列通项公式,即可求得公差和公比,即可求得数列
的通项公式;若选③,结合等差数列前n项和公式、等差数列与等比数列通项公式,即可求得公差和公比,即可求得数列![]() 和
和![]() 的通项公式;
的通项公式;
(2)根据数列![]() 和
和![]() 的通项公式,即可由
的通项公式,即可由![]() 得m,n的关系式
得m,n的关系式![]() ,利用分组求和法即可求得
,利用分组求和法即可求得![]() .
.
(1)若选①:
设等差数列![]() 的公差为d,等比数列
的公差为d,等比数列![]() 的公比为q(
的公比为q(![]() ),
),
则![]() ,
,
解得![]() 或
或![]() (舍),
(舍),
则![]() ,
,![]() ,
,
若选②:
设等差数列![]() 的公差为d,等比数列
的公差为d,等比数列![]() 的公比为q(
的公比为q(![]() ),
),
则由![]() 得
得![]() ,
,
![]() ,又
,又![]() ,
,
![]() ,
,![]() ,
,
![]() .
.
若选③:
设等差数列![]() 的公差为d,等比数列
的公差为d,等比数列![]() 的公比为q(
的公比为q(![]() ),
),
则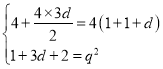 ,解得
,解得![]() 或
或![]() (舍),
(舍),
则![]() ,
,![]() .
.
(2)∵![]() ,
,
∴![]() ,即
,即![]() ,
,
![]()
![]()
![]()
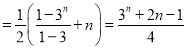 .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果对于函数
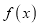 定义域内任意的两个自变量的值
定义域内任意的两个自变量的值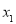 ,
,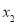 ,当
,当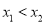 时,都有
时,都有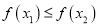 ,且存在两个不相等的自变量值
,且存在两个不相等的自变量值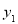 ,
,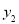 ,使得
,使得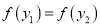 ,就称
,就称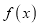 为定义域上的“不严格的增函数”.下列所给的四个函数中为“不严格增函数”的是( )
为定义域上的“不严格的增函数”.下列所给的四个函数中为“不严格增函数”的是( )A.
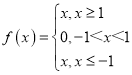 ;B.
;B.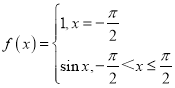 ;
;C.
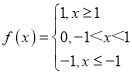 ;D.
;D.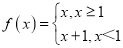 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】在棱长为1的正方体
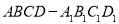 中,已知点P为侧面
中,已知点P为侧面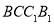 上的一动点,则下列结论正确的是( )
上的一动点,则下列结论正确的是( )A.若点P总保持
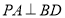 ,则动点P的轨迹是一条线段;
,则动点P的轨迹是一条线段;B.若点P到点A的距离为
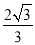 ,则动点P的轨迹是一段圆弧;
,则动点P的轨迹是一段圆弧;C.若P到直线
 与直线
与直线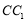 的距离相等,则动点P的轨迹是一段抛物线;
的距离相等,则动点P的轨迹是一段抛物线;D.若P到直线
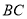 与直线
与直线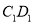 的距离比为
的距离比为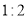 ,则动点P的轨迹是一段双曲线.
,则动点P的轨迹是一段双曲线. -
科目: 来源: 题型:
查看答案和解析>>【题目】双曲线E:
 (
(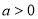 ,
,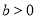 )的左、右焦点分别为
)的左、右焦点分别为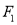 ,
,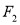 ,已知点
,已知点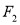 为抛物线C:
为抛物线C: 的焦点,且到双曲线E的一条渐近线的距离为
的焦点,且到双曲线E的一条渐近线的距离为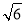 ,又点P为双曲线E上一点,满足
,又点P为双曲线E上一点,满足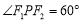 .则
.则(1)双曲线的标准方程为______;
(2)
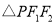 的内切圆半径与外接圆半径之比为______.
的内切圆半径与外接圆半径之比为______. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四棱锥
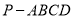 中,底面
中,底面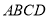 为直角梯形,
为直角梯形,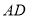 ∥
∥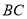 ,
,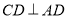 ,
, ,平面
,平面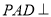 平面
平面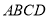 ,
,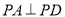 ,
, .
.
(1)求证:
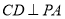 ;
;(2)求二面角
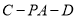 的余弦值.
的余弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】某摄影协会在2019年10月举办了主题“庆祖国70华诞——我们都是追梦人”摄影图片展.通过平常人的镜头,记录了国强民富的幸福生活,向祖国母亲70岁的生日献了一份厚礼.摄影协会收到了来自社会各界的大量作品,从众多照片中选取100张照片展出,其参赛者年龄集中在
 之间,根据统计结果,做出频率分布直方图如下:
之间,根据统计结果,做出频率分布直方图如下: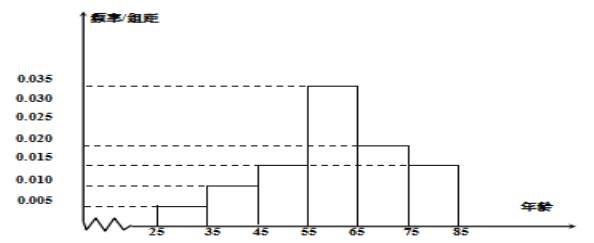
(1)求这100位作者年龄的样本平均数
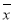 和样本方差
和样本方差 (同一组数据用该区间的中点值作代表);
(同一组数据用该区间的中点值作代表);(2)由频率分布直方图可以认为,作者年龄X服从正态分布
 ,其中
,其中 近似为样本平均数
近似为样本平均数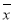 ,
,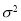 近似为样本方差
近似为样本方差 .
.(i)利用该正态分布,求
 ;
;附:
 ,若
,若 ,则
,则 ,
, ,
, .
.(ii)摄影协会从年龄在
 和
和 的作者中,按照分层抽样的方法,抽出了7人参加“讲述图片背后的故事”座谈会,现要从中选出3人作为代表发言,设这3位发言者的年龄落在区间
的作者中,按照分层抽样的方法,抽出了7人参加“讲述图片背后的故事”座谈会,现要从中选出3人作为代表发言,设这3位发言者的年龄落在区间 的人数是Y,求变量Y的分布列和数学期望.
的人数是Y,求变量Y的分布列和数学期望. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知直线l:
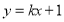 与曲线C:
与曲线C: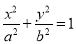 (
(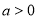 ,
,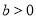 )交于不同的两点A,B,O为坐标原点.
)交于不同的两点A,B,O为坐标原点.(1)若
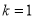 ,
,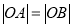 ,求证:曲线C是一个圆;
,求证:曲线C是一个圆;(2)若曲线C过
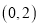 、
、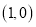 ,是否存在一定点Q,使得
,是否存在一定点Q,使得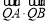 为定值?若存在,求出定点Q和定值;若不存在,请说明理由.
为定值?若存在,求出定点Q和定值;若不存在,请说明理由.
相关试题

