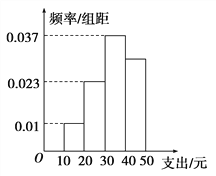
【题目】学校为了解学生在课外读物方面的支出情况,抽取了n名同学进行调查,结果显示这些同学的支出都在[10,50)(单位:元),其中支出在[30,50)(单位:元)的同学有67人,其频率分布直方图如图所示,则n的值为( )
A. 100 B. 120 C. 130 D. 390
参考答案:
【答案】A
【解析】试题分析:根据小矩形的面积之和,算出位于10~30的2组数的频率之和为0.33,从而得到位于30~50的数据的频率之和为1﹣0.33=0.67,再由频率计算公式即可算出样本容量n的值.
解:∵位于10~20、20~30的小矩形的面积分别为
S1=0.01×10=0.1,S2=0.023×10=0.23,
∴位于10~20、20~30的据的频率分别为0.1、0.23
可得位于10~30的前3组数的频率之和为0.1+0.23=0.33
由此可得位于30~50数据的频率之和为1﹣0.33=0.67
∵支出在[30,50)的同学有67人,即位于30~50的频数为67,
∴根据频率计算公式,可得![]() =0.67,解之得n=100
=0.67,解之得n=100
故选:A
-
科目: 来源: 题型:
查看答案和解析>>【题目】(文科)某出租车公司响应国家节能减排的号召,已陆续购买了140辆纯电动汽车作为运营车辆,目前我国主流纯电动汽车按续驶里程数
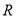 (单位:公里)分为3类,即
(单位:公里)分为3类,即 ,
,  ,
,  .对这140辆车的行驶总里程进行统计,结果如下表:
.对这140辆车的行驶总里程进行统计,结果如下表:
(1)从这140辆汽车中任取1辆,求该车行驶总里程超过5万公里的概率; (2)公司为了了解这些车的工作状况,决定抽取14辆车进行车况分析,按表中描述的六种情况进行分层抽样,设从
 类车中抽取了
类车中抽取了 辆车. (ⅰ)求
辆车. (ⅰ)求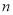 的值; (ⅱ)如果从这
的值; (ⅱ)如果从这 辆车中随机选取2辆车,求恰有1辆车行驶总里程超过5万公里的概率.
辆车中随机选取2辆车,求恰有1辆车行驶总里程超过5万公里的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】(文科)已知函数
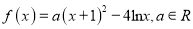 .
.(1)若
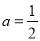 ,求曲线
,求曲线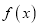 在点
在点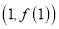 处的切线方程;
处的切线方程;(2)若对任意
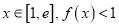 恒成立,求实数
恒成立,求实数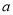 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】(文科)在下列结论中①“
 ”为真是“
”为真是“ ”为真的充分不必要条件;②“
”为真的充分不必要条件;②“  ”为假是“
”为假是“ ”为真的充分不必要条件;③“
”为真的充分不必要条件;③“  ”为真是“
”为真是“ ”为假的充分不必要条件;④“
”为假的充分不必要条件;④“  ” 为真是“
” 为真是“ ”为假充分不必要条件.正确的是__________.
”为假充分不必要条件.正确的是__________. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=asin2x+bcos2x(ab≠0),有下列四个命题:其中正确命题的序号为(填上所有正确命题的序号)
①若a=1,b=﹣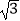 ,要得到函数y=f(x)的图象,只需将函数y=2sin2x的图象向右平移
,要得到函数y=f(x)的图象,只需将函数y=2sin2x的图象向右平移  个单位;
个单位;
②若a=1,b=﹣1,则函数y=f(x)的一个对称中心为( ,0);
,0);
③若y=f(x)的一条对称轴方程为x= ,则a=b;
,则a=b;
④若方程asin2x+bcos2x=m的正实数根从小到大依次构成一个等差数列,则这个等差数列的公差为π. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 ,其中
,其中 且
且 ,若
,若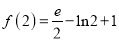 ,
,  在
在 处切线的斜率为
处切线的斜率为 .
.(1)求函数
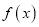 的解析式及其单调区间;
的解析式及其单调区间;(2)若实数
 满足
满足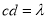 ,且
,且 对于任意
对于任意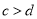 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】某车间共有
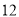 名工人,随机抽取6名,他们某日加工零件个数的茎叶图如图所示,其中茎为十位数,叶为个位数.
名工人,随机抽取6名,他们某日加工零件个数的茎叶图如图所示,其中茎为十位数,叶为个位数. 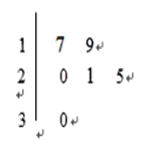
(Ⅰ) 根据茎叶图计算样本均值;
(Ⅱ) 日加工零件个数大于样本均值的工人为优秀工人,根据茎叶图推断该车间
 名工人中有几名优秀工人;
名工人中有几名优秀工人;(Ⅲ) 从该车间
 名工人中,任取2人,求恰有1名优秀工人的概率.
名工人中,任取2人,求恰有1名优秀工人的概率.
相关试题

