【题目】已知函数f(x)=x2+ax+b(a,b∈R)的值域为[0,+∞),若关于x的不等式f(x)<c的解集为(m,m+6),则实数c的值为 .
参考答案:
【答案】9
【解析】解:∵函数f(x)=x2+ax+b(a,b∈R)的值域为[0,+∞),
∴f(x)=x2+ax+b=0只有一个根,即△=a2﹣4b=0则b= ![]()
不等式f(x)<c的解集为(m,m+6),
即为x2+ax+ ![]() <c解集为(m,m+6),
<c解集为(m,m+6),
则x2+ax+ ![]() ﹣c=0的两个根为m,m+6
﹣c=0的两个根为m,m+6
∴|m+6﹣m|= ![]() =6
=6
解得c=9
故答案为:9
根据函数的值域求出a与b的关系,然后根据不等式的解集可得f(x)=c的两个根为m,m+6,最后利用根与系数的关系建立等式,解之即可.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点A(0,﹣2),椭圆E:
 =1(a>b>0)的离心率为
=1(a>b>0)的离心率为 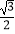 ,F是椭圆的焦点,直线AF的斜率为
,F是椭圆的焦点,直线AF的斜率为  ,O为坐标原点.
,O为坐标原点.
(1)求E的方程;
(2)设过点A的直线l与E相交于P,Q两点,当△OPQ的面积最大时,求l的方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知两定点A(2,5),B(-2,1),M(在第一象限)和N是过原点的直线l上的两个动点,且|MN|=
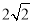 ,l∥AB,如果直线AM和BN的交点C在y轴上,求点C的坐标.
,l∥AB,如果直线AM和BN的交点C在y轴上,求点C的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知△ABC中,BC边上的高所在的直线方程为x﹣2y+1=0,∠A的角平分线所在的直线方程为y=0,点C的坐标为(1,2).
(1)求点A和点B的坐标;
(2)又过点C作直线l与x轴、y轴的正半轴分别交于点M,N,求△MON的面积最小值及此时直线l的方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知等差数列{an}满足a2=2,a5=8.
(1)求{an}的通项公式;
(2)各项均为正数的等比数列{bn}中,b1=1,b2+b3=a4 , 求{bn}的前n项和Tn . -
科目: 来源: 题型:
查看答案和解析>>【题目】如图(1),在正方形SG1G2G3中,E、F分别是G1G2、G2G3的中点,D是EF的中点,现沿SE、SF及EF把这个正方形折成一个几何体如图(2),使G1、G2、G3三点重合于点G.证明:

(1)G在平面SEF上的射影为△SEF的垂心;
(2)求二面角G﹣SE﹣F的正弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知a>0,a≠1,设p:函数y=loga(x+1)在(0,+∞)上单调递减;q:曲线y=x2+(2a﹣3)x+1与x轴交于不同的两点.如果p且q为假命题,p或q为真命题,求a的取值范围.
相关试题

