搜索
【题目】已知两定点A（2，5），B（-2，1），M（在第一象限）和N是过原点的直线l上的两个动点，且|MN|=
，l∥AB，如果直线AM和BN的交点C在y轴上，求点C的坐标.
参考答案：
【答案】C(0,-3)
【解析】试题分析：由点A、B的坐标并利用斜率公式得kAB=1,求出l的方程，设M（a，a）（a＞0），N（b，b）利用｜MN｜=
，求出|a-b|=2，得C的坐标，再由BN的方程得C的坐标，由坐标相同解方程即可.
试题解析：
由点A、B的坐标并利用斜率公式得kAB=1,于是k1=1，从而l的方程为y=x，设M（a，a）（a＞0），N（b，b），由｜MN｜=
，得
，
故|a-b|=2，直线AM的方程为y-5=
(x-2)，令x=0，则得C的坐标为(0, 
)，
直线BN的方程为y-1=
(x+2)，令x=0，则得C的坐标为(0, 
)，故
，化简得a=-b，将其代入|a-b|=2，并注意到a＞0，得a=1，b=-1,∴C(0,-3).
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知点A(m－1,2)，B(1,1)，C(3，m2－m－1)．
(1)若A，B，C三点共线，求实数m的值；
(2)若AB⊥BC，求实数m的值．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图所示，正方体ABCD﹣A′B′C′D′的棱长为1，E、F分别是棱AA′，CC′的中点，过直线EF的平面分别与棱BB′、DD′交于M、N，设BM=x，x∈[0，1]，给出以下四个命题：
①平面MENF⊥平面BDD′B′；
②当且仅当x=
时，四边形MENF的面积最小；
③四边形MENF周长l=f（x），x∈0，1]是单调函数；
④四棱锥C′﹣MENF的体积v=h（x）为常函数；
以上命题中真命题的序号为 ．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知点A（0，﹣2），椭圆E：
=1（a＞b＞0）的离心率为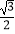 
，F是椭圆的焦点，直线AF的斜率为 
，O为坐标原点．
（1）求E的方程；
（2）设过点A的直线l与E相交于P，Q两点，当△OPQ的面积最大时，求l的方程． -
科目： 来源： 题型：
查看答案和解析>>【题目】已知△ABC中，BC边上的高所在的直线方程为x﹣2y+1=0，∠A的角平分线所在的直线方程为y=0，点C的坐标为（1，2）．
（1）求点A和点B的坐标；
（2）又过点C作直线l与x轴、y轴的正半轴分别交于点M，N，求△MON的面积最小值及此时直线l的方程． -
科目： 来源： 题型：
查看答案和解析>>【题目】已知函数f（x）=x2+ax+b（a，b∈R）的值域为[0，+∞），若关于x的不等式f（x）＜c的解集为（m，m+6），则实数c的值为 ．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知等差数列{an}满足a2=2，a5=8．
（1）求{an}的通项公式；
（2）各项均为正数的等比数列{bn}中，b1=1，b2+b3=a4 ， 求{bn}的前n项和Tn ．
相关试题
