【题目】已知函数![]() .
.
(Ⅰ)求函数![]() 的单调区间;
的单调区间;
(Ⅱ)若对任意![]() ,都有
,都有![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
参考答案:
【答案】(1)f(x)在(-∞,- ![]() )上单调递减,在(-
)上单调递减,在(-![]() ,
, ![]() )上单调递增,在(
)上单调递增,在(![]() ,+∞)上单调递减;(2)实数m的取值范围为[1,+∞).
,+∞)上单调递减;(2)实数m的取值范围为[1,+∞).
【解析】试题分析:(Ⅰ)对函数进行求导得![]() ,分别解不等式
,分别解不等式![]() 和
和![]() 可得单调区间;(Ⅱ) 令
可得单调区间;(Ⅱ) 令![]() ,首先得到
,首先得到![]() ,对函数
,对函数![]() 进行二次求导,得到
进行二次求导,得到![]() 在
在![]() 上单调递减,则
上单调递减,则![]() ,对
,对![]() 分为
分为![]() 和
和![]() 两种情形,判断
两种情形,判断![]() 和0的关系,得到
和0的关系,得到![]() 的单调性,进而得到其与
的单调性,进而得到其与![]() 的关系,从而可得结论.
的关系,从而可得结论.
试题解析:(Ⅰ)由已知得![]() ,当
,当![]() ,即
,即![]() 时,
时, ![]() 或
或![]() ;当
;当![]() ,即
,即![]() 时,
时, ![]() ,所以f(x)在
,所以f(x)在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,在
上单调递增,在![]() 上单调递减.
上单调递减.
(Ⅱ)令![]() ,
, ![]() ,
,
由已知可得![]() ,即
,即![]() ,下面只要考虑
,下面只要考虑![]() 的情况即可.
的情况即可.
g′(x)=(2-x2)ex-1-m,令h(x)=(2-x2)ex-1-m,则h′(x)=-(x2+2x-2)ex-1,
因为x≥1,所以x2+2x-2>0,所以h′(x)<0,
所以h(x)在[1,+∞)上单调递减,即g′(x)在[1,+∞)上单调递减,则g′(x)≤g′(1)=1-m.
①当1-m≤0,即m≥1时,此时g′(x)≤0,所以g(x)在[1,+∞)上单调递减,所以g(x)≤g(1)=0,满足条件;
②当1-m>0,即-1≤m<1时,此时g′(1)>0,g′(2)=-2e-m<0,所以存在x0∈(1,2),使得g′(x0)=0,则当1<x<x0时,g′(x)>0;
当x>x0时,g′(x)<0,所以g(x)在[1,x0]上单调递增,在(x0,+∞)上单调递减,
所以当x∈[1,x0]时,g(x)≥g(1)=0,此时不满足条件.
综上所述,实数m的取值范围为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】2017年是内蒙古自治区成立70周年.某市旅游文化局为了庆祝内蒙古自治区成立70周年,举办了第十三届成吉思汗旅游文化周.为了了解该市关注“旅游文化周”居民的年龄段分布,随机抽取了
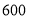 名年龄在
名年龄在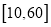 且关注“旅游文化周”的居民进行调查,所得结果统计为如图所示的频率分布直方图.
且关注“旅游文化周”的居民进行调查,所得结果统计为如图所示的频率分布直方图.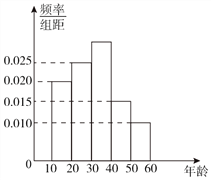
年龄
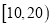
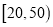
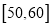
单人促销价格(单位:元)
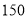
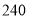
(Ⅰ)根据频率分布直方图,估计该市被抽取市民的年龄的平均数;
(Ⅱ)某旅行社针对“旅游文化周”开展不同年龄段的旅游促销活动,各年龄段的促销价位如表所示.已知该旅行社的运营成本为每人
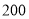 元,以频率分布直方图中各年龄段的频率分布作为参团旅客的年龄频率分布,试通过计算确定该旅行社的这一活动是否盈利;
元,以频率分布直方图中各年龄段的频率分布作为参团旅客的年龄频率分布,试通过计算确定该旅行社的这一活动是否盈利;(Ⅲ)若按照分层抽样的方法从年龄在
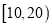 ,
, 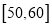 的居民中抽取
的居民中抽取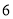 人进行旅游知识推广,并在知识推广后再抽取
人进行旅游知识推广,并在知识推广后再抽取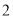 人进行反馈,求进行反馈的居民中至少有
人进行反馈,求进行反馈的居民中至少有 人的年龄在
人的年龄在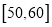 的概率.
的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,底面半径为
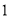 ,母线长为
,母线长为 的圆柱的轴截面是四边形
的圆柱的轴截面是四边形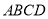 ,线段
,线段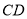 上的两动点
上的两动点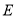 ,
, 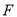 满足
满足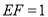 .点
.点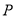 在底面圆
在底面圆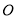 上,且
上,且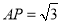 ,
, 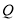 为线段
为线段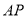 的中点.
的中点. 
(Ⅰ)求证:
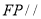 平面
平面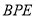 ;
;(Ⅱ)四棱锥
 的体积是否为定值,若是,请求出该定值;若不是,请说明理由.
的体积是否为定值,若是,请求出该定值;若不是,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
 :
:
 的一个焦点与抛物线
的一个焦点与抛物线 的焦点重合,且过点
的焦点重合,且过点 .过点
.过点 的直线
的直线 交椭圆
交椭圆 于
于 ,
,  两点,
两点,  为椭圆的左顶点.
为椭圆的左顶点.(Ⅰ)求椭圆
 的标准方程;
的标准方程;(Ⅱ)求
 面积的最大值,并求此时直线
面积的最大值,并求此时直线 的方程.
的方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系
 中,曲线
中,曲线 的参数方程是
的参数方程是 (
( 为参数),以原点
为参数),以原点 为极点,
为极点,  轴正半轴为极轴,建立极坐标系,直线
轴正半轴为极轴,建立极坐标系,直线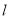 的极坐标方程为
的极坐标方程为 .
.(Ⅰ)求曲线
 的普通方程与直线
的普通方程与直线 的直角坐标方程;
的直角坐标方程;(Ⅱ)已知直线
 与曲线
与曲线 交于
交于 ,
,  两点,与
两点,与 轴交于点
轴交于点 ,求
,求 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
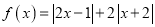 .
.(Ⅰ)求函数
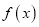 的最小值;
的最小值;(Ⅱ)解不等式

-
科目: 来源: 题型:
查看答案和解析>>【题目】现有
 六支足球队参加单循环比赛(即任意两支球队只踢一场比赛),第一周的比赛中
六支足球队参加单循环比赛(即任意两支球队只踢一场比赛),第一周的比赛中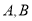 ,各踢了
,各踢了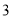 场,
场, 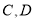 各踢了
各踢了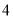 场,
场, 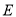 踢了
踢了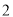 场,且
场,且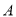 队与
队与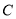 队未踢过,
队未踢过, 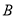 队与
队与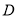 队也未踢过,则在第一周的比赛中,
队也未踢过,则在第一周的比赛中, 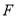 队踢的比赛的场数是( )
队踢的比赛的场数是( )A.
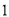 B.
B. 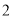 C.
C. 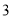 D.
D. 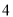
相关试题

