【题目】已知函数.

(Ⅰ)求函数的最小值；

(Ⅱ)解不等式

【答案】（1）5；（2）.

【解析】试题分析：⑴利用绝对值不等式的性质，求得函数的最小值；

⑵方法一：去掉绝对值，写成分段函数的形式，然后求解；方法二：作出函数的图象，数形结合，解不等式

解析：(Ⅰ)因为f(x)＝|2x－1|＋2|x＋2|≥|(2x－1)－2(x＋2)|＝5，

所以

(Ⅱ)解法一：f(x)＝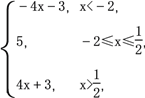

当x<－2时，由－4x－3<8，解得x>－，即－<x<－2；

当－2≤x≤时，5<8恒成立，即－2≤x≤；

当x>时，由4x＋3<8，解得x<，即<x<，

所以原不等式的解集为.

解法二(图象法)：f(x)＝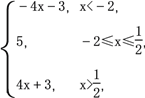

函数f(x)的图象如图所示，

令f(x)＝8，解得x＝－或x＝，

所以不等式f(x)<8的解集为.

关闭