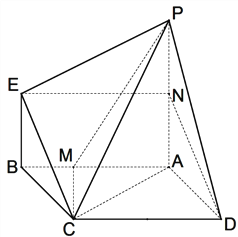
【题目】如图, ![]() 是平行四边行,
是平行四边行, ![]() 平面
平面![]() ,
, ![]() //
// ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.

(1)证明: ![]() //平面
//平面![]() ;
;
(2)求证:平面![]() 平面
平面![]() ;
;
(3)求直线![]() 与平面
与平面![]() 所成角的正弦值;
所成角的正弦值;
(4)求二面角![]() 的平面角的正切值.
的平面角的正切值.
参考答案:
【答案】(1)详见解析;(2)详见解析;(3)![]() ;(4)
;(4)![]() .
.
【解析】试题分析:(1)取![]() 的中点
的中点![]() ,连
,连![]() ,
, ![]() ,利用平行四边形得到线线平行,进而利用线面平行的判定定理进行证明;(2)先利用余弦定理、勾股定理证明线线垂直,再利用线面垂直和面面垂直的判定定理进行证明;(3)利用面面垂直的性质作出线面垂直,进而找出线面角;(4)先作出二面角的平面角,再利用直角三角形进行求解.
,利用平行四边形得到线线平行,进而利用线面平行的判定定理进行证明;(2)先利用余弦定理、勾股定理证明线线垂直,再利用线面垂直和面面垂直的判定定理进行证明;(3)利用面面垂直的性质作出线面垂直,进而找出线面角;(4)先作出二面角的平面角,再利用直角三角形进行求解.
试题解析:(1)取![]() 的中点
的中点![]() ,连
,连![]() ,
, ![]() 。由已知
。由已知![]() //
// ![]() ,
, ![]() ,
, ![]() ,
,
则![]() 为平行四边形,所以
为平行四边形,所以![]() //
// ![]()
又![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,
,
所以![]() //平面
//平面![]()
(2)![]() 中,
中, ![]() ,
, ![]()
所以![]()
∴![]() ∴
∴![]()
∵![]() 平面
平面![]()
![]() 平面
平面![]()
∴![]() 又∵
又∵![]() ∴
∴![]() 平面
平面![]()
又![]() 平面
平面![]() ∴平面
∴平面![]() 平面
平面![]()
(3)作![]() 于
于![]() ,连
,连![]() ,可证
,可证![]() 平面
平面![]()
![]() 为
为![]() 与平面
与平面![]() 所成角
所成角
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
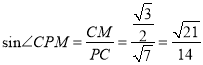 。
。
答: 直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() 。
。
(4)![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 ,
,  .
.(Ⅰ)当
 时,
时,  恒成立,求
恒成立,求 的取值范围;
的取值范围;(Ⅱ)当
 时,研究函数
时,研究函数 的零点个数;
的零点个数;(Ⅲ)求证:
 (参考数据:
(参考数据:  ).
). -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=x2+(a+8)x+a2+a﹣12(a<0),且f(a2﹣4)=f(2a﹣8),则
 的最小值为( )
的最小值为( )
A.
B.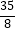
C.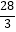
D.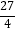
-
科目: 来源: 题型:
查看答案和解析>>【题目】继共享单车之后,又一种新型的出行方式------“共享汽车”也开始亮相北上广深等十余大中城市,一款叫“一度用车”的共享汽车在广州提供的车型是“奇瑞eQ”,每次租车收费按行驶里程加用车时间,标准是“1元/公里+0.1元/分钟”,李先生家离上班地点10公里,每天租用共享汽车上下班,由于堵车因素,每次路上开车花费的时间是一个随机变量,根据一段时间统计40次路上开车花费时间在各时间段内的情况如下:
时间(分钟)

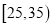
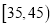


次数
8
14
8
8
2
以各时间段发生的频率视为概率,假设每次路上开车花费的时间视为用车时间,范围为
 分钟.
分钟.(Ⅰ)若李先生上.下班时租用一次共享汽车路上开车不超过45分钟,便是所有可选择的交通工具中的一次最优选择,设
 是4次使用共享汽车中最优选择的次数,求
是4次使用共享汽车中最优选择的次数,求 的分布列和期望.
的分布列和期望.(Ⅱ)若李先生每天上下班使用共享汽车2次,一个月(以20天计算)平均用车费用大约是多少(同一时段,用该区间的中点值作代表).
-
科目: 来源: 题型:
查看答案和解析>>【题目】函数f(x)的定义域为D,满足:①f(x)在D内是单调函数;②存在[
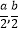 ]D,使得f(x)在[
]D,使得f(x)在[ 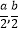 ]上的值域为[a,b],那么就称函数y=f(x)为“优美函数”,若函数f(x)=logc(cx﹣t)(c>0,c≠1)是“优美函数”,则t的取值范围为( )
]上的值域为[a,b],那么就称函数y=f(x)为“优美函数”,若函数f(x)=logc(cx﹣t)(c>0,c≠1)是“优美函数”,则t的取值范围为( )
A.(0,1)
B.(0, )
)
C.(﹣∞, )
)
D.(0, )
) -
科目: 来源: 题型:
查看答案和解析>>【题目】甲乙丙丁四个物体同时从某一点出发向同一个方向运动,其路程fi(x)(i=1,2,3,4)关于时间x(x≥0)的函数关系式分别为
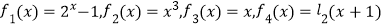 , 有以下结论:
, 有以下结论:
①当x>1时,甲在最前面;
②当x>1时,乙在最前面;
③当0<x<1时,丁在最前面,当x>1时,丁在最后面;
④丙不可能在最前面,也不可能最最后面;
⑤如果它们已知运动下去,最终在最前面的是甲.
其中,正确结论的序号为(把正确结论的序号都填上,多填或少填均不得分) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,隔河看两目标A、B,但不能到达,在岸边选取相距
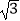 km的C、D两点,并测得∠ACB=75°,∠BCD=45°,∠ADC=30°,∠ADB=45°(A、B、C、D在同一平面内),求两目标A、B之间的距离.
km的C、D两点,并测得∠ACB=75°,∠BCD=45°,∠ADC=30°,∠ADB=45°(A、B、C、D在同一平面内),求两目标A、B之间的距离. 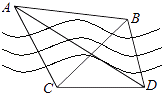
相关试题

