Question

【题目】已知函数f（x）=2|x+1|+|x﹣a|（a∈R）．
（1）若 a=1，求不等式 f（x）≥5的解集；
（2）若函数f（x）的最小值为3，求实数 a的值．

Answer 1

【答案】
（1）解：当 a=1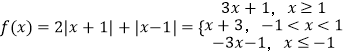， ，当x≥1时，3x+1≥5，即 ，∴ ；

当﹣1＜x＜1时，x+3≥5，即x≥2，此时x无实数解；

当x≤﹣1时，﹣3x﹣1≥5，即x≤﹣2，∴x≤﹣2．

综上所述，不等式的解集为{x|x≤﹣2，或 ．

（2）解：当a=﹣1时，f（x）=3|x+1|最小值为 0，不符合题意，

当a＞﹣1时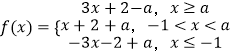， ，∴f（x）min=f（﹣1）=1+a=3，此时a=2；

当a＜﹣1时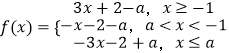， ，f（x）min=f（﹣1）=﹣1﹣a=3，此时a=﹣4．

综上所示，a=2或a=﹣4．

【解析】（1）把f（x）写成分段函数的形式，分类讨论，分别求得不等式 f（x）≥5的解集，综合可得结论．（2）分当a=﹣1时、当a＞﹣1时、当a＜﹣1时三种情况，分别求得a的值，综合可得结论．
【考点精析】本题主要考查了绝对值不等式的解法的相关知识点，需要掌握含绝对值不等式的解法：定义法、平方法、同解变形法，其同解定理有；规律：关键是去掉绝对值的符号才能正确解答此题．