【题目】已知0<a<1,函数f(x)=loga(ax﹣1)
(I)求函数f(x)的定义域;
(Ⅱ)判断f(x)的单调性;
(Ⅲ)若m满足f(1﹣m)≥f(1﹣m2),求m的范围.
参考答案:
【答案】解:(Ⅰ)由ax﹣1>0,得ax>1,
因为0<a<1,所以x<0,
所以f(x)定义域为(﹣∞,0)
(Ⅱ)设y=logaU,U=ax﹣1
因为0<a<1,y=logaU是减函数,U=ax﹣1是减函数,
所以 ![]() 是(﹣∞,0)上的增函数
是(﹣∞,0)上的增函数
(Ⅲ)由(2)知f(x)是(﹣∞,0)上的增函数,
所以 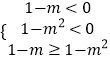 ,解得:m>1
,解得:m>1
【解析】(Ⅰ)根据对数函数的性质求出函数的定义域即可;(Ⅱ)根据复合函数同增异减的原则,结合换元法判断出f(x)的单调性即可;(Ⅲ)根据函数的单调性以及对数函数的性质得到关于m的不等式组,解出即可.
【考点精析】掌握对数函数的定义域和对数函数的单调区间是解答本题的根本,需要知道对数函数的定义域范围:(0,+∞);a变化对图象的影响:在第一象限内,a越大图象越靠低;在第四象限内,a越大图象越靠高.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=x2+bx+c,其图象与y轴的交点为(0,1),且满足f(1﹣x)=f(1+x).
(1)求f(x);
(2)设
 ,m>0,求函数g(x)在[0,m]上的最大值;
,m>0,求函数g(x)在[0,m]上的最大值;(3)设h(x)=lnf(x),若对于一切x∈[0,1],不等式h(x+1﹣t)<h(2x+2)恒成立,求实数t的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在四棱锥P﹣ABCD中,底面ABCD是棱长为2的正方形,侧面PAD为正三角形,且面PAD⊥面ABCD,E、F分别为棱AB、PC的中点.
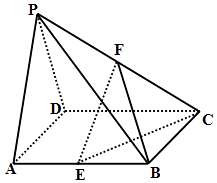
(1)求证:EF∥平面PAD;
(2)求三棱锥B﹣EFC的体积;
(3)求二面角P﹣EC﹣D的正切值. -
科目: 来源: 题型:
查看答案和解析>>【题目】设集合A={x|2﹣5≤2﹣x≤4},B={x|x2+2mx﹣3m2<0,m>0}.
(1)若m=2,求A∩B;
(2)若BA,求实数m的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某蔬菜基地种植西红柿,由历年市场行情得知,从二月一日起的300天内,西红柿场售价与上市时间的关系如图一的一条折线表示;西红柿的种植成本与上市时间的关系如图二的抛物线段表示.
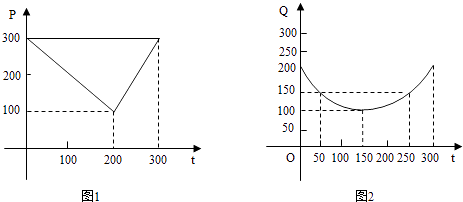
(1)写出图一表示的市场售价与时间的函数关系式p=f(t);写出图二表示的种植成本与时间的函数关系式Q=g(t);
(2)认定市场售价减去种植成本为纯收益,问何时上市的西红柿纯收益最大?(注:市场售价各种植成本的单位:元/102㎏,时间单位:天) -
科目: 来源: 题型:
查看答案和解析>>【题目】若命题p:曲线
 =1为双曲线,命题q:函数f(x)=(4﹣a)x在R上是增函数,且p∨q为真命题,p∧q为假命题,则实数a的取值范围是 .
=1为双曲线,命题q:函数f(x)=(4﹣a)x在R上是增函数,且p∨q为真命题,p∧q为假命题,则实数a的取值范围是 . -
科目: 来源: 题型:
查看答案和解析>>【题目】已知
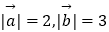 ,
, 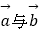 的夹角为60°,
的夹角为60°, 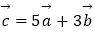 ,
, 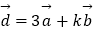 ,当实数k为何值时,
,当实数k为何值时,
(1)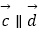
(2)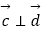 .
.
相关试题

