【题目】已知函数f(x)=(![]() )x.
)x.
(Ⅰ)当x∈[﹣1,1]时,求函数y=[f(x)]2﹣2af(x)+3的最小值g(a);
(Ⅱ)在(Ⅰ)的条件下,是否存在实数m>n>3,使得g(x)的定义域为[n,m],值域为[n2,m2]?若存在,求出m、n的值;若不存在,请说明理由.
参考答案:
【答案】(Ⅰ)g(a)=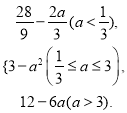 (Ⅱ)见解析.
(Ⅱ)见解析.
【解析】试题分析:(Ⅰ)在![]() 的情况下,求出
的情况下,求出![]() 的值域,对所给函数进行配方化简,可利用一元二次函数的性质对
的值域,对所给函数进行配方化简,可利用一元二次函数的性质对![]() 进行分类讨论,可得函数的最小值
进行分类讨论,可得函数的最小值![]() ;(Ⅱ)假设存在,利用(Ⅰ)中分段函数在
;(Ⅱ)假设存在,利用(Ⅰ)中分段函数在![]() 的单调性,结合区间与值域,可得关于
的单调性,结合区间与值域,可得关于![]() 的等式,解得
的等式,解得![]() 存在情况.
存在情况.
试题解析:(Ⅰ)∵x∈[﹣1,1],∴f(x)=(![]() )x∈[
)x∈[![]() ,3],
,3],
y=[f(x)]2﹣2af(x)+3=[(![]() )x]2﹣2a(
)x]2﹣2a(![]() )x+3
)x+3
=[(![]() )x﹣a]2+3﹣a2. .
)x﹣a]2+3﹣a2. .
由一元二次函数的性质分三种情况:
若a<![]() ,则当
,则当![]() 时,ymin=g(a)=
时,ymin=g(a)=![]() ;
;
若![]() ≤a≤3,则当
≤a≤3,则当![]() 时,ymin=g(a)=3﹣a2;
时,ymin=g(a)=3﹣a2;
若a>3,则当![]() 时,ymin=g(a)=12﹣6a.
时,ymin=g(a)=12﹣6a.
∴g(a)=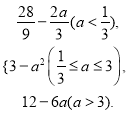
(Ⅱ)假设存在满足题意的m、n,
∵m>n>3,且g(x)=12﹣6x在区间(3,+∞)内是减函数,
又g(x)的定义域为[n,m],值域为[n2,m2],
∴![]()
两式相减,得6(m﹣n)=(m+n)(m﹣n),
∵m>n>3,∴m+n=6,但这与“m>n>3”矛盾,
∴满足题意的m、n不存在.
-
科目: 来源: 题型:
查看答案和解析>>【题目】选修4—4:坐标系与参数方程
在平面直角坐标系
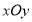 中,直线
中,直线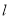 的参数方程为
的参数方程为 (
( 为参数).以原点为极点,
为参数).以原点为极点,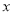 轴正半轴为极轴建立极坐标系,圆
轴正半轴为极轴建立极坐标系,圆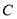 的方程为
的方程为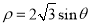 .
.(Ⅰ)写出直线
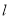 的普通方程和圆
的普通方程和圆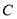 的直角坐标方程;
的直角坐标方程;(Ⅱ)若点
 的直角坐标为
的直角坐标为 ,圆
,圆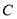 与直线
与直线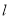 交于
交于 两点,求
两点,求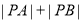 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】三国魏人刘徽,自撰《海岛算经》,专论测高望远.其中有一题:今有望海岛,立两表齐,高三丈,前後相去千步,令後表与前表相直。从前表却行一百二十三步,人目著地取望岛峰,与表末参合。从後表却行百二十七步,人目著地取望岛峰,亦与表末参合。问岛高及去表各几何?翻译如下:要测量海岛上一座山峰
 的高度
的高度 ,立两根高三丈的标杆
,立两根高三丈的标杆 和
和 ,前后两竿相距
,前后两竿相距 步,使后标杆杆脚
步,使后标杆杆脚 与前标杆杆脚
与前标杆杆脚 与山峰脚
与山峰脚 在同一直线上,从前标杆杆脚
在同一直线上,从前标杆杆脚 退行
退行 步到
步到 ,人眼著地观测到岛峰,
,人眼著地观测到岛峰, 、
、 、
、 、三点共线,从后标杆杆脚
、三点共线,从后标杆杆脚 退行
退行 步到
步到 ,人眼著地观测到岛峰,
,人眼著地观测到岛峰, 、
、 、
、 三点也共线,则山峰的高度
三点也共线,则山峰的高度 __________步.(古制
__________步.(古制 步
步 尺,
尺, 里
里 丈
丈 尺
尺 步)
步) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在三棱柱
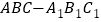 中,侧面
中,侧面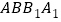 ,
,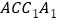 均为正方形,
均为正方形,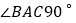 ,点
,点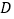 是棱
是棱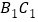 的中点.请建立适当的坐标系,求解下列问题:
的中点.请建立适当的坐标系,求解下列问题: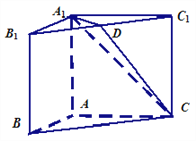
(Ⅰ)求证:异面直线
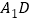 与
与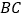 互相垂直;
互相垂直;(Ⅱ)求二面角(钝角)
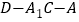 的余弦值.
的余弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】函数
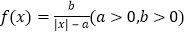 的图象形如汉字“囧”,故称其为“囧函数”.
的图象形如汉字“囧”,故称其为“囧函数”.下列命题:
①“囧函数”的值域为
 ;
;②“囧函数”在
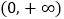 上单调递增;
上单调递增;③“囧函数”的图象关于
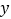 轴对称;
轴对称;④“囧函数”有两个零点;
⑤“囧函数”的图象与直线
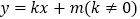
至少有一个交点.正确命题的个数为( )
A. 1 B. 2 C. 3 D. 4
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 .
.(Ⅰ)求函数
 的单调区间;
的单调区间;(Ⅱ)求证:①
 ;
;②曲线
 上的所有点都落在圆
上的所有点都落在圆 内.
内. -
科目: 来源: 题型:
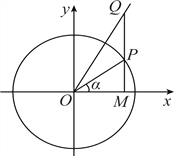
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,点P是单位圆上的动点,过点P作x轴的垂线与射线y=
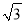 x(x≥0)交于点Q,与x轴交于点M.记∠MOP=α,且α∈(﹣
x(x≥0)交于点Q,与x轴交于点M.记∠MOP=α,且α∈(﹣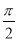 ,
, 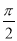 ).
).
(Ⅰ)若sinα=
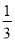 ,求cos∠POQ;
,求cos∠POQ;(Ⅱ)求△OPQ面积的最大值.
相关试题

