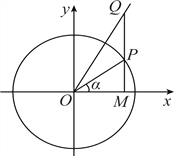
【题目】如图,在平面直角坐标系xOy中,点P是单位圆上的动点,过点P作x轴的垂线与射线y=![]() x(x≥0)交于点Q,与x轴交于点M.记∠MOP=α,且α∈(﹣
x(x≥0)交于点Q,与x轴交于点M.记∠MOP=α,且α∈(﹣![]() ,
, ![]() ).
).
(Ⅰ)若sinα=![]() ,求cos∠POQ;
,求cos∠POQ;
(Ⅱ)求△OPQ面积的最大值.
参考答案:
【答案】(Ⅰ)![]() ;(Ⅱ)
;(Ⅱ)![]() .
.
【解析】试题分析:(Ⅰ)由角![]() 的正弦值可得其余弦值,再用
的正弦值可得其余弦值,再用![]() 角表示
角表示![]() ,可由两角差的余弦公式可得角的余值;(Ⅱ)由三角函数的定义可得
,可由两角差的余弦公式可得角的余值;(Ⅱ)由三角函数的定义可得![]() 点的坐标,再利用
点的坐标,再利用![]() 的正余弦值表示三角形的面积,利用三角函数的性质可得其最值,即为三角形面积的最大值.
的正余弦值表示三角形的面积,利用三角函数的性质可得其最值,即为三角形面积的最大值.
试题解析:(Ⅰ)因为![]() ,且
,且![]() 所以
所以![]() .
.
所以![]() .
.
(Ⅱ)由三角函数定义,得P(cosα,sinα),从而![]() ,
,
所以![]()
![]()

 .
.
因为![]() 所以当
所以当![]() 时,取等号,
时,取等号,
所以△OPQ面积的最大值为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=(
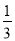 )x.
)x.(Ⅰ)当x∈[﹣1,1]时,求函数y=[f(x)]2﹣2af(x)+3的最小值g(a);
(Ⅱ)在(Ⅰ)的条件下,是否存在实数m>n>3,使得g(x)的定义域为[n,m],值域为[n2,m2]?若存在,求出m、n的值;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】函数
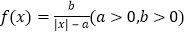 的图象形如汉字“囧”,故称其为“囧函数”.
的图象形如汉字“囧”,故称其为“囧函数”.下列命题:
①“囧函数”的值域为
 ;
;②“囧函数”在
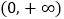 上单调递增;
上单调递增;③“囧函数”的图象关于
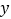 轴对称;
轴对称;④“囧函数”有两个零点;
⑤“囧函数”的图象与直线
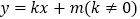
至少有一个交点.正确命题的个数为( )
A. 1 B. 2 C. 3 D. 4
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 .
.(Ⅰ)求函数
 的单调区间;
的单调区间;(Ⅱ)求证:①
 ;
;②曲线
 上的所有点都落在圆
上的所有点都落在圆 内.
内. -
科目: 来源: 题型:
查看答案和解析>>【题目】某工厂修建一个长方体无盖蓄水池,其容积为6400立方米,深度为4米.池底每平方米的造价为120元,池壁每平方米的造价为100元.设池底长方形的长为x米.
(Ⅰ)求底面积,并用含x的表达式表示池壁面积;
(Ⅱ)怎样设计水池能使总造价最低?最低造价是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】设L为曲线C:y=
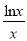 在点(1,0)处的切线.
在点(1,0)处的切线.(1)求L的方程;
(2)证明:除切点(1,0)之外,曲线C在直线L的下方.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知幂函数
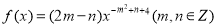 为偶函数,且在区间
为偶函数,且在区间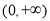 上是单调递增函数。
上是单调递增函数。(Ⅰ)求函数
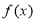 的解析式;
的解析式;(Ⅱ)设
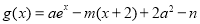 ,若
,若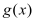 能取遍
能取遍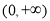 内的所有实数,求实数
内的所有实数,求实数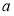 的取值范围.
的取值范围.
相关试题

