【题目】已知函数![]() ,令
,令![]() ,其中
,其中![]() 是函数
是函数![]() 的导函数.
的导函数.
(Ⅰ)当![]() 时,求
时,求![]() 的极值;
的极值;
(Ⅱ)当![]() 时,若存在
时,若存在![]() ,使得
,使得![]() 恒成立,求
恒成立,求![]() 的取值范围.
的取值范围.
参考答案:
【答案】(Ⅰ) 极小值![]() ,无极大值;(Ⅱ)
,无极大值;(Ⅱ)![]() .
.
【解析】
试题分析:(Ⅰ)把![]() 代入函数
代入函数![]() 的解析式,求其导函数,由导函数的零点对定义域分段,得到函
的解析式,求其导函数,由导函数的零点对定义域分段,得到函
数在各区间段内的单调性,从而求得函数极值;(Ⅱ)由函数的导函数可得函数的单调性,求得函数在![]() 上的最值,再由
上的最值,再由![]() 恒成立,结合分离参数可得
恒成立,结合分离参数可得![]() ,构造函数
,构造函数![]() ,利用导数求其最值得
,利用导数求其最值得![]() 的范围.
的范围.
试题解析:(Ⅰ)依题意![]() ,则
,则![]()
当a=0时,![]()
令![]() 解得
解得![]() ;
;
当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]()
所以![]() 的单调递减区间为(0,
的单调递减区间为(0,![]() ),单调递增区间为(
),单调递增区间为(![]() ,+∞)
,+∞)
所以![]() 时
时![]() 取得极小值
取得极小值![]() ,无极大值.
,无极大值.
(Ⅱ)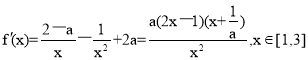
当![]() 即
即![]() 时,恒有
时,恒有![]() 成立,
成立,
所以![]() 在[1,3]上是单调递减.
在[1,3]上是单调递减.
所以![]()
所以![]() ,
,
因为存在![]() ,使得
,使得![]() 恒成立,
恒成立,
所以![]() 整理得
整理得
![]()
又![]() <0,所以
<0,所以![]()
令![]() =-
=-![]() ,则
,则![]() ∈(2,8),构造函数
∈(2,8),构造函数![]() ,
,
所以![]() ,
,
当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() ,此时函数单调递增,
,此时函数单调递增,
当![]() 时,
时,![]() ,此时函数单调递减,
,此时函数单调递减,
所以![]() ,
,
所以m的取值范围为(![]() ,+∞).
,+∞).
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
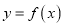 的图象由图中的两条射线和抛物线的一部分组成,求函数的解析式.
的图象由图中的两条射线和抛物线的一部分组成,求函数的解析式.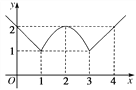
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知f(x)是二次函数,且满足f(0)=1,f(x+1)-f(x)=2x,求f(x).
-
科目: 来源: 题型:
查看答案和解析>>【题目】求下列函数解析式:
(1)已知
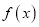 是一次函数,且满足3
是一次函数,且满足3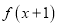 -
-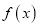 =
=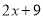 ,求
,求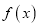 ;
;(2)已知
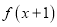 =
=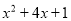 ,求
,求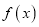 的解析式.
的解析式. -
科目: 来源: 题型:
查看答案和解析>>【题目】随着生活水平的提高,越来越多的人参与了潜水这项活动。某潜水中心调查了100名男姓与100名女姓下潜至距离水面5米时是否会耳鸣,下图为其等高条形图:
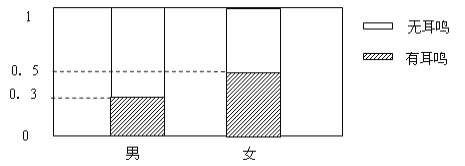
绘出2×2列联表;
②根据列联表的独立性检验,能否在犯错误的概率不超过0.05的前提下认为耳鸣与性别有关系?
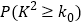
0.025
0.010
0.005
0.001
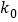
5.024
6.635
7.879
10.828
附:
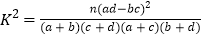
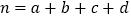
-
科目: 来源: 题型:
查看答案和解析>>【题目】在中学生综合素质评价某个维度的测评中,分“优秀、合格、尚待改进”三个等级进行学生互评.某校高一年级有男生500人,女生400人,为了了解性别对该维度测评结果的影响,采用分层抽样方法从高一年级抽取了45名学生的测评结果,并作出频数统计表如下:
表1:男生

表2:女生

(1)从表二的非优秀学生中随机选取2人交谈,求所选2人中恰有1人测评等级为合格的概率;
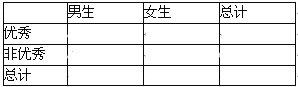
(2)由表中统计数据填写下边2×2列联表,并判断是否有90%的把握认为“测评结果优秀与性别有关”.
参考数据与公式:
K2=
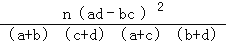 ,其中n=a+b+c+d.
,其中n=a+b+c+d.临界值表:

-
科目: 来源: 题型:
查看答案和解析>>【题目】函数f(x)是定义在[-1,0)∪(0,1]上的奇函数,当x∈[-1,0)时,f(x)=2x+
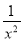 (x∈R).
(x∈R).(1)当x∈(0,1]时,求f(x)的解析式.
(2)判断f(x)在(0,1]上的单调性,并证明你的结论.
相关试题

