【题目】已知圆C:(x﹣1)2+(y﹣2)2=25,直线l:(2m+1)x+(m+1)y﹣7m﹣4=0(m∈R).
(1)证明:不论m取什么实数时,直线l与圆恒交于两点;
(2)求直线l被圆C截得的线段的最短长度以及此时直线l的方程.
参考答案:
【答案】
(1)解:由m(2x+y﹣7)+(x+y﹣4)=0知直线l恒过定点,
又 ![]() ,
,
∴直线l恒过定点A(3,1),
且(3﹣1)2+(1﹣2)2=5<25A(3,1)必在圆内,
故直线l与圆恒有两交点
(2)解:∵圆心为C(1,2),定点为A(3,1)
∴ ![]()
由平面几何知识知,当直线l与AC垂直时所截线段最短,此时kl=2
∴l方程为:y﹣1=2(x﹣3)2x﹣y﹣5=0,此时 ![]()
∴最短弦长= ![]()
【解析】(1)把直线l的方程变形后,根据直线l恒过定点,得到关于x与y的二元一次方程组,求出方程组的解即为直线l恒过的定点坐标,然后利用两点间的距离公式求出此点到圆心的距离d,发现d小于圆的半径,得到此点在圆内,故直线l与圆恒交于两点;(2)由平面几何知识可知,当直线l与AC垂直时,所截取的线段最短,由圆心C和定点A的坐标求出直线AC的斜率,根据两直线垂直时斜率的乘积为﹣1,求出直线l的斜率,由A的坐标和求出的斜率写出直线l的方程,再由A与C的坐标,利用两点间的距离公式求出|AC|即为弦心距,根据圆的半径,弦心距及弦的一半构成的直角三角形,利用勾股定理即可求出此时的弦长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知正三棱锥P﹣ABC,点P,A,B,C都在半径为
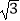 的球面上,若PA,PB,PC两两垂直,则球心到截面ABC的距离为 .
的球面上,若PA,PB,PC两两垂直,则球心到截面ABC的距离为 . -
科目: 来源: 题型:
查看答案和解析>>【题目】函数y=lg(3﹣4x+x2)的定义域为M,当x∈M时,则f(x)=2x+2﹣3×4x的最大值为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】设函数
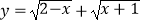 的定义域为A,函数y=log2(a﹣x)的定义域为B.
的定义域为A,函数y=log2(a﹣x)的定义域为B.
(1)若AB,求实数a的取值范围;
(2)设全集为R,若非空集合(RB)∩A的元素中有且只有一个是整数,求实数a的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,角A,B,C所对的边分别为a,b,c且b=c,∠A的平分线为AD,若
 =m
=m 
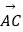 .
.
(1)当m=2时,求cosA
(2)当 ∈(1,
∈(1,  )时,求实数m的取值范围.
)时,求实数m的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知圆C:x2+y2﹣4x﹣6y+12=0,点A(3,5).
(1)求过点A的圆的切线方程;
(2)O点是坐标原点,连接OA,OC,求△AOC的面积S. -
科目: 来源: 题型:
查看答案和解析>>【题目】将一张纸沿直线l对折一次后,点A(0,4)与点B(8,0)重叠,点C(6,8)与点D(m,n)重叠.
(1)求直线l的方程;
(2)求m+n的值;
(3)直线l上是否存在一点P,使得||PB|﹣|PC||存在最大值,如果存在,请求出最大值,以及此时点P的坐标;如果不存在,请说明理由.
相关试题

