【题目】函数y=lg(3﹣4x+x2)的定义域为M,当x∈M时,则f(x)=2x+2﹣3×4x的最大值为 .
参考答案:
【答案】![]()
【解析】解:函数y=lg(3﹣4x+x2)的定义域为M, ∴3﹣4x+x2>0,即(x﹣1)(x﹣3)>0,
解得M={x|x>3或x<1},
∴f(x)=2x+2﹣3×4x , 令2x=t,0<t<2或t>8,
∴f(t)=﹣3t2+t+2=﹣3(t﹣ ![]() )2+
)2+ ![]() ,
,
当t= ![]() 时,f(t)取最大值,
时,f(t)取最大值,
f(x)max=f( ![]() )=
)= ![]() ,
,
所以答案是: ![]() ;
;
【考点精析】利用函数的定义域及其求法和函数的最值及其几何意义对题目进行判断即可得到答案,需要熟知求函数的定义域时,一般遵循以下原则:①![]() 是整式时,定义域是全体实数;②
是整式时,定义域是全体实数;②![]() 是分式函数时,定义域是使分母不为零的一切实数;③
是分式函数时,定义域是使分母不为零的一切实数;③![]() 是偶次根式时,定义域是使被开方式为非负值时的实数的集合;④对数函数的真数大于零,当对数或指数函数的底数中含变量时,底数须大于零且不等于1,零(负)指数幂的底数不能为零;利用二次函数的性质(配方法)求函数的最大(小)值;利用图象求函数的最大(小)值;利用函数单调性的判断函数的最大(小)值.
是偶次根式时,定义域是使被开方式为非负值时的实数的集合;④对数函数的真数大于零,当对数或指数函数的底数中含变量时,底数须大于零且不等于1,零(负)指数幂的底数不能为零;利用二次函数的性质(配方法)求函数的最大(小)值;利用图象求函数的最大(小)值;利用函数单调性的判断函数的最大(小)值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】f(x)=x2﹣2x,g(x)=ax+2(a>0),若对任意的x1∈[﹣1,2],存在x0∈[﹣1,2],使g(x1)=f(x0),则a的取值范围是( )
A.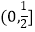
B.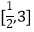
C.[3,+∞)
D.(0,3] -
科目: 来源: 题型:
查看答案和解析>>【题目】某餐厅装修,需要大块胶合板
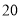 张,小块胶合板
张,小块胶合板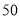 张,已知市场出售
张,已知市场出售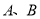 两种不同规格的胶合板。经过测算,
两种不同规格的胶合板。经过测算, 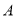 种规格的胶合板可同时截得大块胶合板
种规格的胶合板可同时截得大块胶合板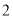 张,小块胶合板
张,小块胶合板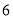 张,
张, 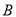 种规格的胶合板可同时截得大块胶合板
种规格的胶合板可同时截得大块胶合板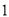 张,小块胶合板
张,小块胶合板 张.已知
张.已知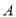 种规格胶合板每张
种规格胶合板每张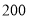 元,
元, 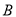 种规格胶合板每张
种规格胶合板每张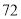 元.分别用
元.分别用 表示购买
表示购买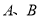 两种不同规格的胶合板的张数.
两种不同规格的胶合板的张数.(1)用
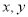 列出满足条件的数学关系式,并画出相应的平面区域;
列出满足条件的数学关系式,并画出相应的平面区域;(2)根据施工需求,
 两种不同规格的胶合板各买多少张花费资金最少?并求出最少资金数.
两种不同规格的胶合板各买多少张花费资金最少?并求出最少资金数. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知正三棱锥P﹣ABC,点P,A,B,C都在半径为
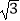 的球面上,若PA,PB,PC两两垂直,则球心到截面ABC的距离为 .
的球面上,若PA,PB,PC两两垂直,则球心到截面ABC的距离为 . -
科目: 来源: 题型:
查看答案和解析>>【题目】设函数
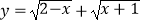 的定义域为A,函数y=log2(a﹣x)的定义域为B.
的定义域为A,函数y=log2(a﹣x)的定义域为B.
(1)若AB,求实数a的取值范围;
(2)设全集为R,若非空集合(RB)∩A的元素中有且只有一个是整数,求实数a的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知圆C:(x﹣1)2+(y﹣2)2=25,直线l:(2m+1)x+(m+1)y﹣7m﹣4=0(m∈R).
(1)证明:不论m取什么实数时,直线l与圆恒交于两点;
(2)求直线l被圆C截得的线段的最短长度以及此时直线l的方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,角A,B,C所对的边分别为a,b,c且b=c,∠A的平分线为AD,若
 =m
=m 
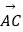 .
.
(1)当m=2时,求cosA
(2)当 ∈(1,
∈(1,  )时,求实数m的取值范围.
)时,求实数m的取值范围.
相关试题

