【题目】双曲线![]() 的离心率为2,右焦点
的离心率为2,右焦点![]() 到它的一条渐近线的距离为
到它的一条渐近线的距离为![]() 。
。
(1)求双曲线的标准方程;
(2)是否存在过点![]() 且与双曲线的右支角不同的
且与双曲线的右支角不同的![]() 两点的直线
两点的直线![]() ,当点满足
,当点满足![]() 时,使得点
时,使得点![]() 在直线
在直线![]() 上的射影点
上的射影点![]() 满足
满足![]() ?若存在,求出直线
?若存在,求出直线![]() 的方程;若不存在,说明理由。
的方程;若不存在,说明理由。
参考答案:
【答案】(1) ![]() (2) 存在这样的直线
(2) 存在这样的直线![]() 满足条件,其方程为
满足条件,其方程为![]() 或
或![]()
【解析】试题分析:(1)由点到直线的距离公式可知: ![]() ,结合
,结合![]() 即可求得
即可求得![]() ,进而根据离心率可得
,进而根据离心率可得![]() ,从而求得方程;
,从而求得方程;
(2)(2)假设存在满足条件的直线l,直线l的斜率不存在时,求得N,P,Q坐标,由![]() ,此时
,此时![]() 不满足条件;当斜率存在时,设l的方程为y=k(x-2),代入双曲线方程,由韦达定理及向量的数量积的坐标表示
不满足条件;当斜率存在时,设l的方程为y=k(x-2),代入双曲线方程,由韦达定理及向量的数量积的坐标表示![]() ,即
,即![]() ,代入即可求得k的值,求得直线方程.
,代入即可求得k的值,求得直线方程.
试题解析:
(1)双曲线![]() 焦点在x轴上,设右焦点为(c,0),一条渐近线为bx-ay=0.
焦点在x轴上,设右焦点为(c,0),一条渐近线为bx-ay=0.
由点到直线的距离公式可知: ![]() ,由
,由![]() ,解得
,解得![]() .
.
由双曲线的离心率为![]() ,解得
,解得![]() .
.
所以,双曲线的方程为![]() .
.
(2)因为![]() ,所以
,所以![]() 是
是![]() 的中点,
的中点,
假设存在满足条件的直线![]() ,
,
若直线![]() 的斜率不存在时,此时点
的斜率不存在时,此时点![]() 即为
即为![]() ,可解得
,可解得![]() ,
,
所以![]() ,所以
,所以![]() ,此时
,此时![]() 不满足条件。
不满足条件。
若直线![]() 的斜率存在时,设斜率为
的斜率存在时,设斜率为![]() ,则
,则![]() 的方程为
的方程为![]() ,联立
,联立![]() ,
,
得![]() ,要使得
,要使得![]() 与双曲线交于右支的不同的
与双曲线交于右支的不同的![]() 两点,
两点,
须要![]() ,即
,即![]() ,可得
,可得![]() ,
,
又![]() ,所以
,所以![]()
又因为![]() 在直线
在直线![]() 上的射影为
上的射影为![]() 满足
满足![]() ,
,
所以![]() ,
,
所以![]() ,
,
即![]() ,
,
可得![]() 或
或![]() ,又因为
,又因为![]() ,所以
,所以![]() ,即
,即![]() ,
,
所以存在这样的直线![]() 满足条件,其方程为
满足条件,其方程为![]() 或
或![]() 。
。
-
科目: 来源: 题型:
查看答案和解析>>【题目】中国古代的数学家们最早发现并应用勾股定理,而最先对勾股定理进行证明的是三国时期的数学家赵爽.赵爽创制了一幅“勾股圆方图”,用数形结合的方法,给出了勾股定理的详细证明。在这幅“勾股圆方图”中,
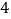 个相等的直角三角形再加上中间的那个小正方形组成一个大的正方形。若直角三角形的较小锐角
个相等的直角三角形再加上中间的那个小正方形组成一个大的正方形。若直角三角形的较小锐角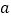 的正切值为
的正切值为 ,现向该正方形区域内投掷-枚飞镖,则飞镖落在小正方形内(阴影部分)的概率是( )
,现向该正方形区域内投掷-枚飞镖,则飞镖落在小正方形内(阴影部分)的概率是( )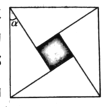
A.
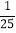 B.
B. 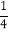
C.
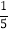 D.
D. 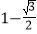
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
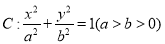 的两个焦点分别为
的两个焦点分别为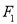 ,
, 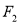 ,离心率为
,离心率为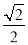 ,且过点
,且过点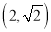 .
.(
 )求椭圆
)求椭圆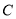 的标准方程.
的标准方程.(
 )
)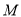 、
、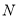 、
、 、
、 是椭圆
是椭圆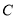 上的四个不同的点,两条都不和
上的四个不同的点,两条都不和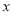 轴垂直的直线
轴垂直的直线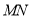 和
和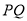 分别过点
分别过点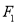 ,
, 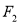 ,且这条直线互相垂直,求证:
,且这条直线互相垂直,求证: 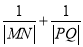 为定值.
为定值. -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面四边形
 中,
中,  ,
,  ,将
,将 沿
沿 折起,使得平面
折起,使得平面 平面
平面 ,如图.
,如图.
(1)求证:
 ;
;(2)若
 为
为 中点,求直线
中点,求直线 与平面
与平面 所成角的正弦值.
所成角的正弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】(1)求过点
 ,斜率是直线
,斜率是直线 的斜率的
的斜率的 的直线方程;
的直线方程;(2)求经过点
 ,且在
,且在 轴上的截距等于在
轴上的截距等于在 轴上截距的2倍的直线方程.
轴上截距的2倍的直线方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,过底面是矩形的四棱锥FABCD的顶点F作EF∥AB,使AB=2EF,且平面ABFE⊥平面ABCD,若点G在CD上且满足DG=G
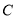 .
.
求证:(1)FG∥平面AED;
(2)平面DAF⊥平面BAF.
-
科目: 来源: 题型:
查看答案和解析>>【题目】网购已经成为一种时尚,商家为了鼓励消费,购买时在店铺领取优惠券,买后给予好评返还现金等促销手段.经统计,近五年某店铺用于促销的费用
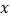 (万元)与当年度该店铺的销售收人
(万元)与当年度该店铺的销售收人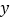 (万元)的数据如下表:
(万元)的数据如下表:年份
2013年
2014年
2015年
2016年
2017年
促销费用
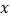
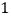
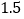
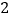
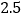
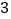
销售收入
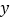
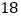
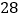
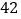
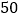
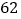
(1)请根据上表提供的数据,用最小二乘法求出/span>
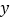 关于
关于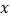 的线性回归方
的线性回归方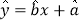 ;
;(2)2018年度该店铺预测销售收人至少达到
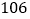 万元,则该店铺至少准备投入多少万元的促销费?
万元,则该店铺至少准备投入多少万元的促销费?参考公式:
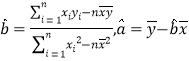
参考数据:
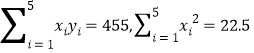
相关试题

