【题目】如图,过底面是矩形的四棱锥FABCD的顶点F作EF∥AB,使AB=2EF,且平面ABFE⊥平面ABCD,若点G在CD上且满足DG=G![]() .
.

求证:(1)FG∥平面AED;
(2)平面DAF⊥平面BAF.
参考答案:
【答案】(1)见解析;(2)见解析.
【解析】试题分析: (1)根据题意证明四边形DEFG为平行四边形,则FG∥ED,由线面平行判定定理,结论易证得;(2)由面面垂直的性质定理证明AD⊥平面BAF,由面面垂直的判定定理易证出结论.
试题解析:
(1)证明:(1) ![]() DG=GC,AB=CD=2EF,AB∥EF∥CD,
DG=GC,AB=CD=2EF,AB∥EF∥CD,
![]() EF∥DG,EF=DG.
EF∥DG,EF=DG.
![]() 四边形DEFG为平行四边形,
四边形DEFG为平行四边形,
![]() FG∥ED.
FG∥ED.
又![]() FG∥平面AED,ED平面AED,
FG∥平面AED,ED平面AED,
![]() FG∥平面AED.
FG∥平面AED.
(2) ![]() 平面ABFE⊥平面ABCD,平面ABFE∩平面ABCD=AB,
平面ABFE⊥平面ABCD,平面ABFE∩平面ABCD=AB,
AD⊥AB,AD平面ABCD,
![]() AD⊥平面BAF,
AD⊥平面BAF,
又![]() AD平面DAF,
AD平面DAF,
![]() 平面DAF⊥平面BAF.
平面DAF⊥平面BAF.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面四边形
 中,
中,  ,
,  ,将
,将 沿
沿 折起,使得平面
折起,使得平面 平面
平面 ,如图.
,如图.
(1)求证:
 ;
;(2)若
 为
为 中点,求直线
中点,求直线 与平面
与平面 所成角的正弦值.
所成角的正弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】双曲线
 的离心率为2,右焦点
的离心率为2,右焦点 到它的一条渐近线的距离为
到它的一条渐近线的距离为 。
。(1)求双曲线的标准方程;
(2)是否存在过点
 且与双曲线的右支角不同的
且与双曲线的右支角不同的 两点的直线
两点的直线 ,当点满足
,当点满足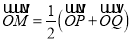 时,使得点
时,使得点 在直线
在直线 上的射影点
上的射影点 满足
满足 ?若存在,求出直线
?若存在,求出直线 的方程;若不存在,说明理由。
的方程;若不存在,说明理由。 -
科目: 来源: 题型:
查看答案和解析>>【题目】(1)求过点
 ,斜率是直线
,斜率是直线 的斜率的
的斜率的 的直线方程;
的直线方程;(2)求经过点
 ,且在
,且在 轴上的截距等于在
轴上的截距等于在 轴上截距的2倍的直线方程.
轴上截距的2倍的直线方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】网购已经成为一种时尚,商家为了鼓励消费,购买时在店铺领取优惠券,买后给予好评返还现金等促销手段.经统计,近五年某店铺用于促销的费用
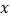 (万元)与当年度该店铺的销售收人
(万元)与当年度该店铺的销售收人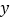 (万元)的数据如下表:
(万元)的数据如下表:年份
2013年
2014年
2015年
2016年
2017年
促销费用
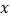
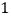
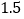
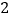
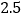
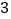
销售收入
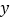
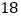
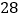
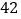
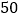
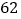
(1)请根据上表提供的数据,用最小二乘法求出/span>
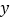 关于
关于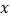 的线性回归方
的线性回归方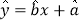 ;
;(2)2018年度该店铺预测销售收人至少达到
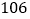 万元,则该店铺至少准备投入多少万元的促销费?
万元,则该店铺至少准备投入多少万元的促销费?参考公式:
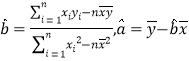
参考数据:
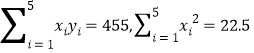
-
科目: 来源: 题型:
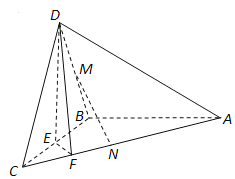
查看答案和解析>>【题目】如图,在三棱锥
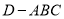 中,已知
中,已知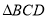 是正三角形,
是正三角形,  平面
平面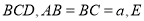 为
为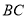 的中点,
的中点, 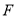 在棱
在棱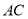 上,且
上,且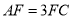 .
.
(1)求三棱锥
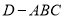 的体积;
的体积;(2)求证:
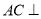 平面
平面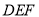 ;
;(3)若
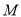 为
为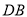 中点,
中点,  在棱
在棱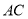 上,且
上,且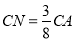 ,求证:
,求证: 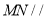 平面
平面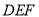 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,已知以M为圆心的圆M:
 及其上一点A(2,4)
及其上一点A(2,4)
(1)设圆N与x轴相切,与圆M外切,且圆心N在直线x=6上,求圆N的标准方程;
(2)设平行于OA的直线l与圆M相交于B、C两点,且BC=OA,求直线l的方程;
(3)设点T(t,o)满足:存在圆M上的两点P和Q,使得
 ,求实数t的取值范围。
,求实数t的取值范围。
相关试题

