【题目】已知椭圆![]() 的两个焦点分别为
的两个焦点分别为![]() ,
, ![]() ,离心率为
,离心率为![]() ,且过点
,且过点![]() .
.
(![]() )求椭圆
)求椭圆![]() 的标准方程.
的标准方程.
(![]() )
)![]() 、
、![]() 、
、![]() 、
、![]() 是椭圆
是椭圆![]() 上的四个不同的点,两条都不和
上的四个不同的点,两条都不和![]() 轴垂直的直线
轴垂直的直线![]() 和
和![]() 分别过点
分别过点![]() ,
, ![]() ,且这条直线互相垂直,求证:
,且这条直线互相垂直,求证: ![]() 为定值.
为定值.
参考答案:
【答案】(![]() )
)![]() (
(![]() )见解析
)见解析
【解析】试题分析:
(1)由离心率可得![]() ,故椭圆的方程为
,故椭圆的方程为![]() ,将点
,将点![]() 的坐标代入方程可得
的坐标代入方程可得![]() ,
, ![]() ,从而可得椭圆的方程。(2)①当直线
,从而可得椭圆的方程。(2)①当直线![]() 的斜率为0时,
的斜率为0时, ![]() 为长轴长,
为长轴长, ![]() 为通径长;②当直线
为通径长;②当直线![]() 的斜率不为0时,设出直线
的斜率不为0时,设出直线![]() 的方程,运用椭圆的弦长公式可得
的方程,运用椭圆的弦长公式可得![]() 和
和![]() ,然后验证即可得到结论。
,然后验证即可得到结论。
试题解析:
(![]() )∵
)∵ ![]() ,
,
∴ ![]() ,
,
∴ ![]() ,
,
∴ 椭圆![]() 的方程为
的方程为![]() ,
,
又点![]() 在椭圆上,
在椭圆上,
∴ ![]()
解得![]() ,
,
∴ ![]() ,
,
∴ 椭圆![]() 的方程为
的方程为![]() .
.
(![]() )由(1)得椭圆
)由(1)得椭圆![]() 的焦点坐标为
的焦点坐标为![]() ,
, ![]() ,
,
①当直线![]() 的斜率为0时,则
的斜率为0时,则![]() ,
,
∴ 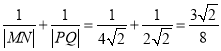 .
.
②当直线![]() 的斜率为0时,设其
的斜率为0时,设其![]() ,
,
由直线![]() 与
与![]() 互相垂直,可得直线
互相垂直,可得直线![]() ,
,
由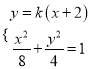 消去y整理得
消去y整理得![]() ,
,
设![]() ,
, ![]() ,
,
则![]() ,
, ![]() ,
,
∴ ![]() ,
,
同理![]() ,
,
∴ 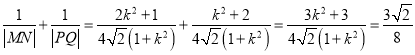 .
.
综上可得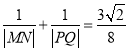 为定值。
为定值。
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点
 在函数
在函数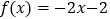 的图象上,数列
的图象上,数列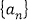 的前
的前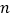 项和为
项和为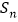 ,数列
,数列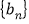 的前
的前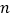 项和为
项和为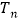 ,且
,且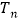 是
是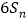 与
与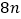 的等差中项.
的等差中项.(
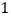 )求数列
)求数列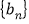 的通项公式.
的通项公式.(
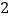 )设
)设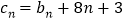 ,数列
,数列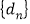 满足
满足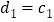 ,
,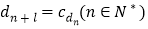 .求数列
.求数列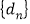 的前
的前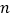 项和
项和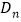 .
.(
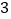 )在(
)在(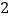 )的条件下,设
)的条件下,设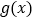 是定义在正整数集上的函数,对于任意的正整数
是定义在正整数集上的函数,对于任意的正整数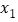 ,
, ,恒有
,恒有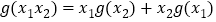 成立,且
成立,且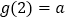 (
(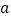 为常数,
为常数,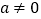 ),试判断数列
),试判断数列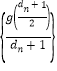 是否为等差数列,并说明理由.
是否为等差数列,并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】中国在超级计算机方面发展迅速,跻身国际先进水平国家,预报天气的准确度也大大提高,天气预报说今后的三天中,每一天下雨的概率都是
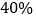 ,我们可以通过随机模拟的方法估计概率.我们先产生
,我们可以通过随机模拟的方法估计概率.我们先产生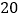 组随机数
组随机数907 966 191 925 271 932 812 458 569 683
431 257 393 027 556 488 730 113 537 989
在这组数中,用
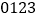 表示下雨,
表示下雨,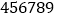 表示不下雨,那么今后的三天中都下雨的概率近似为( )
表示不下雨,那么今后的三天中都下雨的概率近似为( )A.
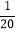 B.
B.  C.
C. 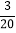 D.
D. 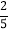
-
科目: 来源: 题型:
查看答案和解析>>【题目】中国古代的数学家们最早发现并应用勾股定理,而最先对勾股定理进行证明的是三国时期的数学家赵爽.赵爽创制了一幅“勾股圆方图”,用数形结合的方法,给出了勾股定理的详细证明。在这幅“勾股圆方图”中,
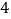 个相等的直角三角形再加上中间的那个小正方形组成一个大的正方形。若直角三角形的较小锐角
个相等的直角三角形再加上中间的那个小正方形组成一个大的正方形。若直角三角形的较小锐角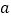 的正切值为
的正切值为 ,现向该正方形区域内投掷-枚飞镖,则飞镖落在小正方形内(阴影部分)的概率是( )
,现向该正方形区域内投掷-枚飞镖,则飞镖落在小正方形内(阴影部分)的概率是( )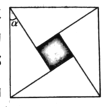
A.
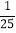 B.
B. 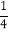
C.
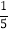 D.
D. 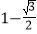
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面四边形
 中,
中,  ,
,  ,将
,将 沿
沿 折起,使得平面
折起,使得平面 平面
平面 ,如图.
,如图.
(1)求证:
 ;
;(2)若
 为
为 中点,求直线
中点,求直线 与平面
与平面 所成角的正弦值.
所成角的正弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】双曲线
 的离心率为2,右焦点
的离心率为2,右焦点 到它的一条渐近线的距离为
到它的一条渐近线的距离为 。
。(1)求双曲线的标准方程;
(2)是否存在过点
 且与双曲线的右支角不同的
且与双曲线的右支角不同的 两点的直线
两点的直线 ,当点满足
,当点满足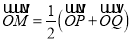 时,使得点
时,使得点 在直线
在直线 上的射影点
上的射影点 满足
满足 ?若存在,求出直线
?若存在,求出直线 的方程;若不存在,说明理由。
的方程;若不存在,说明理由。 -
科目: 来源: 题型:
查看答案和解析>>【题目】(1)求过点
 ,斜率是直线
,斜率是直线 的斜率的
的斜率的 的直线方程;
的直线方程;(2)求经过点
 ,且在
,且在 轴上的截距等于在
轴上的截距等于在 轴上截距的2倍的直线方程.
轴上截距的2倍的直线方程.
相关试题

