【题目】各项均为正数的等比数列![]() 满足
满足![]() ,
, ![]() .
.
(Ⅰ)求数列![]() 的通项公式;
的通项公式;
(Ⅱ)若 ,求数列
,求数列![]() 的前
的前![]() 项和
项和![]() .
.
参考答案:
【答案】(Ⅰ)![]() ;(Ⅱ)
;(Ⅱ)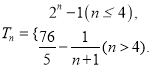
【解析】试题分析:(1)通过![]() ,
, ![]() 及数列
及数列![]() 的各项均为正数,可得
的各项均为正数,可得![]() ,计算即可;(2)
,计算即可;(2)![]() 时;利用分组求和与等比数列求和,
时;利用分组求和与等比数列求和, ![]() 通过
通过![]()
![]()
![]() ,可得
,可得![]()
![]() ,利用错位相减法及等比数列的求和公式计算即可.
,利用错位相减法及等比数列的求和公式计算即可.
试题解析:(Ⅰ)设等比数列![]() 的公比为
的公比为![]() ,由
,由![]() 得
得
由![]() ,得
,得![]() 或
或![]() ,
,
![]() 数列
数列![]() 为正项数列,
为正项数列, ![]() ,
,
代入①,得![]() ,
, ![]() .
.
(Ⅱ)由(Ⅰ)知当![]() 时,
时, ![]()
![]()
![]() ,
,
此时![]()
![]() ,
,
当![]() 时,
时, ![]()
![]()
![]()
![]() .
.
当![]() 时,
时,
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.
综上可知,数列![]() 的前
的前![]() 项和
项和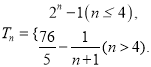
【方法点晴】裂项相消法是最难把握的求和方法之一,其原因是有时很难找到裂项的方向,突破这一难点的方法是根据式子的结构特点,掌握一些常见的裂项技巧:①![]() ;②
;②![]()
![]() ;③
;③![]() ;
;
④ ;此外,需注意裂项之后相消的过程中容易出现丢项或多项的问题,导致计算结果错误.
;此外,需注意裂项之后相消的过程中容易出现丢项或多项的问题,导致计算结果错误.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点
 在椭圆
在椭圆 :
:  (
( )上,设
)上,设 ,
,  ,
,  分别为左顶点、上顶点、下顶点,且下顶点
分别为左顶点、上顶点、下顶点,且下顶点 到直线
到直线 的距离为
的距离为 .
.(Ⅰ)求椭圆
 的方程;
的方程;(Ⅱ)设点
 ,
,  (
( )为椭圆
)为椭圆 上两点,且满足
上两点,且满足 ,求证:
,求证:  的面积为定值,并求出该定值.
的面积为定值,并求出该定值. -
科目: 来源: 题型:
查看答案和解析>>【题目】用简单随机抽样方法从含有6个个体的总体中,抽取一个容量为2的样本,某一个体a“第一次被抽到的概率”、“第二次被抽到的概率”、“在整个抽样过程中被抽到”的概率分别是
. -
科目: 来源: 题型:
查看答案和解析>>【题目】2016年高一新生入学后,为了了解新生学业水平,某区对新生进行了水平测试,随机抽取了50名新生的成绩,其相关数据统计如下:
分数段
频数
选择题得分24分以上(含24分)
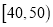
5
2
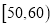
10
4
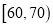
15
12
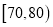
10
6
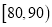
5
4
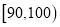
5
5
(Ⅰ)若从分数在
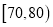 ,
, 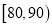 的被调查的新生中各随机选取2人进行追踪调查,求恰好有2名新生选择题得分不足24分的概率;
的被调查的新生中各随机选取2人进行追踪调查,求恰好有2名新生选择题得分不足24分的概率;(Ⅱ)在(Ⅰ)的条件下,记选中的4名新生中选择题得分不足24分的人数为
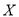 ,求随机变量
,求随机变量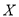 的分布列和数学期望.
的分布列和数学期望. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=lnx﹣
 a(x﹣1)(a∈R).
a(x﹣1)(a∈R).
(1)若a=﹣2,求曲线y=f(x)在点(1,f(1))处的切线方程;
(2)若不等式f(x)<0对任意x∈(1,+∞)恒成立. (ⅰ)求实数a的取值范围;
(ⅱ)试比较ea﹣2与ae﹣2的大小,并给出证明(e为自然对数的底数,e=2.71828). -
科目: 来源: 题型:
查看答案和解析>>【题目】已知在四面体ABCD中,E,F分别是AC,BD的中点,若AB=2,CD=4,EF⊥AB,则EF与CD所成的角的度数为( )
A.90°
B.45°
C.60°
D.30° -
科目: 来源: 题型:
查看答案和解析>>【题目】一盒中装有各色球12只,其中5个红球,4个黑球,2个白球,1个绿球;从中随机取出1球.求:
(1)取出的1球是红球或黑球的概率;
(2)取出的1球是红球或黑球或白球的概率.
相关试题

