【题目】经市场调查,某种商品在过去50天的销量和价格均为销售时间t(天)的函数,且销售量近似地满足f(t)=-2t+200(1≤t≤50,t∈N),前30天价格为g(t)=![]() t+30(1≤t≤30,t∈N),后20天价格为g(t)=45(31≤t≤50,t∈N).
t+30(1≤t≤30,t∈N),后20天价格为g(t)=45(31≤t≤50,t∈N).
(1)写出该种商品的日销售额S与时间t的函数关系式;
(2)求日销售额S的最大值.
参考答案:
【答案】(1)S=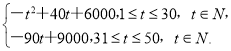 (2)6400.
(2)6400.
【解析】(1)根据题意得
S=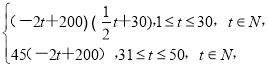
即S=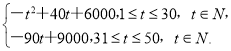
(2)①当1≤t≤30,t∈N时,S=-(t-20)2+6400,
当t=20时,S的最大值为6400;
②当31≤t≤50,t∈N时,S=-90t+9000为减函数,
当t=31时,S的最大值是6210,
∵6210<6400,∴当t=20时,日销售额S有最大值6400.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若有穷数列
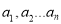 (
(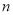 是正整数),满足
是正整数),满足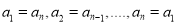 即
即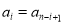 (
(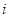 是正整数,且
是正整数,且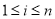 ),就称该数列为“对称数列”。例如,数列
),就称该数列为“对称数列”。例如,数列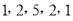 与数列
与数列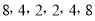 都是“对称数列”.
都是“对称数列”. (1)已知数列
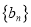 是项数为9的对称数列,且
是项数为9的对称数列,且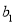 ,
,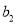 ,
,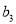 ,
,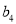 ,
,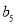 成等差数列,
成等差数列, 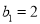 ,
, 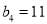 ,试求
,试求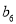 ,
, 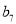 ,
, 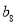 ,
, 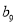 ,并求前9项和
,并求前9项和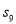 .
.(2)若
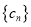 是项数为
是项数为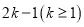 的对称数列,且
的对称数列,且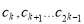 构成首项为31,公差为
构成首项为31,公差为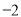 的等差数列,数列
的等差数列,数列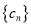 前
前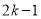 项和为
项和为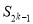 ,则当
,则当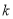 为何值时,
为何值时, 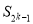 取到最大值?最大值为多少?
取到最大值?最大值为多少?(3)设
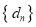 是
是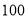 项的“对称数列”,其中
项的“对称数列”,其中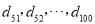 是首项为1,公比为2的等比数列.求
是首项为1,公比为2的等比数列.求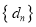 前
前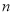 项的和
项的和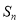
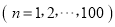 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知{an}是等差数列,满足a1=3,a4=12,数列{bn}满足b1=4,b4=20,且{bn-an}为等比数列.
(1)求数列{an}和{bn}的通项公式;
(2)求数列{bn}的前n项和.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知长方体的长和宽都是
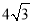 cm,高是4 cm.
cm,高是4 cm.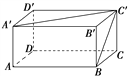
(1)求BC和A′C′所成的角的度数.
(2)求AA′和BC′所成的角的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在
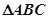 中,根据下列条件解三角形,其中有两个解的是( )
中,根据下列条件解三角形,其中有两个解的是( )A. b="10," A=450, C=600 B. a=6, c=5, B=600
C. a=7, b=5, A=600 D. a=14, b="16," A=450
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆C:
 的左焦点F为圆
的左焦点F为圆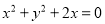 的圆心,且椭圆C上的点到点F的距离最小值为
的圆心,且椭圆C上的点到点F的距离最小值为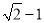 。
。(I)求椭圆C的方程;
(II)已知经过点F的动直线
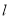 与椭圆C交于不同的两点A、B,点M坐标为(
与椭圆C交于不同的两点A、B,点M坐标为(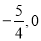 ),证明:
),证明: 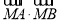 为定值。
为定值。 -
科目: 来源: 题型:
查看答案和解析>>【题目】某公司为了适应市场需求对产品结构做了重大调整,调整后初期利润增长迅速,之后增长越来越慢,若要建立恰当的函数模型来反映该公司调整后利润
 与时间
与时间 的关系,可选用( )
的关系,可选用( )A. 一次函数 B. 二次函数 C. 指数型函数 D. 对数型函数
相关试题

