【题目】对于函数![]() ,若在定义域内存在实数
,若在定义域内存在实数![]() ,满足
,满足![]() ,则称
,则称![]() 为“局部奇函数”.
为“局部奇函数”.
(1)已知二次函数![]() ,试判断
,试判断![]() 是否为“局部奇函数”?并说明理由;
是否为“局部奇函数”?并说明理由;
(2)若![]() 是定义在区间
是定义在区间![]() 上的“局部奇函数”,求实数
上的“局部奇函数”,求实数![]() 的取值范围;
的取值范围;
(3)若![]() 为定义域
为定义域![]() 上的“局部奇函数”,求实数
上的“局部奇函数”,求实数![]() 的取值范围;
的取值范围;
参考答案:
【答案】(1) ![]() 是“局部奇函数”,理由见解析;(2)
是“局部奇函数”,理由见解析;(2) ![]() ;(3)
;(3) ![]()
【解析】试题分析:
(1)结合函数的解析式,当![]() 或
或![]() 时,
时, ![]() 成立,则
成立,则![]() 是“局部奇函数”;
是“局部奇函数”;
(2)由题意换元令![]() 结合对勾函数的性质可得
结合对勾函数的性质可得![]()
(3)由定义得![]() 有解,结合函数的性质分类讨论:①若
有解,结合函数的性质分类讨论:①若![]() 则
则![]()
②若![]() 则
则![]()
故实数![]() 的取值范围是
的取值范围是![]()
试题解析:
(1)由题意得: ![]()
当![]() 或
或![]() 时,
时, ![]() 成立,
成立, ![]() 是“局部奇函数”;
是“局部奇函数”;
(2)由题意得: ![]()
![]() 在
在![]() 有解,
有解, ![]()
令![]() 则
则![]() 设
设![]() 在
在![]() 单调递减,
单调递减,
在![]() 单调递增
单调递增![]()
(3)由定义得![]()
即![]() 有解,
有解,
设![]() 方程等价于
方程等价于![]() 在
在![]() 时有解,
时有解,
设![]() 对称轴
对称轴![]()
①若![]() 则
则![]() 即
即![]() 此时
此时![]()
②若![]() 则
则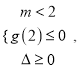 即
即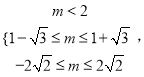 此时
此时![]()
综上得: ![]() 即实数
即实数![]() 的取值范围是
的取值范围是![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知
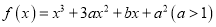 在
在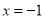 处的极值为0.
处的极值为0.(1)求常数
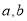 的值;
的值;(2)求
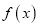 的单调区间;
的单调区间;(3)方程
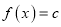 在区间
在区间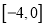 上有三个不同的实根时,求实数
上有三个不同的实根时,求实数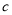 的范围.
的范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
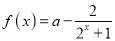 (
(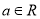 ).
).(1)是否存在实数
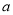 使函数
使函数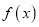 是奇函数?并说明理由;
是奇函数?并说明理由;(2)在(1)的条件下,当
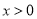 时,
时, 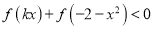 恒成立,求实数
恒成立,求实数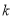 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】在直角坐标系
 中,直线
中,直线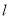 过点
过点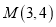 ,其倾斜角为
,其倾斜角为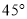 ,以原点为极点,以
,以原点为极点,以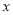 正半轴为极轴建立极坐标,并使得它与直角坐标系
正半轴为极轴建立极坐标,并使得它与直角坐标系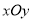 有相同的长度单位,圆
有相同的长度单位,圆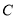 的极坐标方程为
的极坐标方程为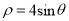 .
.(1)求直线
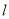 的参数方程和圆
的参数方程和圆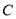 的普通方程;
的普通方程;(2)设圆
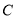 与直线
与直线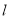 交于点
交于点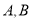 ,求
,求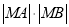 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】某厂生产某种产品的月固定成本为10(万元),每生产
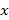 件,需另投入成本为
件,需另投入成本为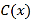 (万元).当月产量不足30件时,
(万元).当月产量不足30件时, 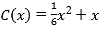 (万元);当月产量不低于30件时,
(万元);当月产量不低于30件时, 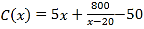 (万元).因设备问题,该厂月生产量不超过50件.现已知此商品每件售价为5万元,且该厂每个月生产的商品都能当月全部销售完.
(万元).因设备问题,该厂月生产量不超过50件.现已知此商品每件售价为5万元,且该厂每个月生产的商品都能当月全部销售完.(1)写出月利润
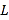 (万元)关于月产量
(万元)关于月产量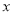 (件)的函数解析式;
(件)的函数解析式;(2)当月产量为多少件时,该厂所获月利润最大?
-
科目: 来源: 题型:
查看答案和解析>>【题目】设直线
 及直线外一点
及直线外一点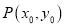 .
.(1)写出点
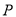 到直线
到直线 的距离公式;
的距离公式;(2)利用向量求证点到直线的距离公式.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
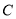 的两个焦点是
的两个焦点是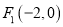 ,
, 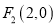 ,且椭圆
,且椭圆 经过点
经过点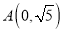 .
.(1)求椭圆
 的标准方程;
的标准方程;(2)若过椭圆
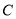 的左焦点
的左焦点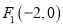 且斜率为1的直线
且斜率为1的直线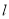 与椭圆
与椭圆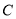 交于
交于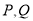 两点,求线段
两点,求线段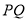 的长.
的长.
相关试题

