【题目】已知函数![]() (
(![]() ).
).
(1)是否存在实数![]() 使函数
使函数![]() 是奇函数?并说明理由;
是奇函数?并说明理由;
(2)在(1)的条件下,当![]() 时,
时, ![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
参考答案:
【答案】(1) ![]() ;(2)
;(2) ![]()
【解析】试题分析:
(1)结合奇函数的性质得到关于a的恒等式,据此可得a=1;
(2)由题意可得函数![]() 在
在![]() 上是增函数.结合函数的性质有
上是增函数.结合函数的性质有![]() 在
在![]() 上是增函数,
上是增函数,
结合函数的性质可得![]() 的取值范围为
的取值范围为![]()
试题解析:
(1)当![]() 函数
函数![]() 是奇函数.
是奇函数.
由![]() 得,
得, ![]() ,
,
解得![]() .
.
(2)函数![]() .
.
任取![]() 设
设![]()
则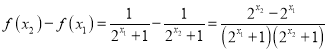 ,
,
因为函数![]() 在
在![]() 上是增函数,且
上是增函数,且![]() 所以
所以![]() ,
,
又![]() ,所以
,所以![]() ,即
,即![]() ,
,
所以函数![]() 在
在![]() 上是增函数.
上是增函数.
因为![]() 是奇函数,从而不等式
是奇函数,从而不等式![]() 等价于
等价于
![]() ,
,
因为函数![]() 在
在![]() 上是增函数,所以
上是增函数,所以![]() ,
,
所以当![]() 时
时![]() 恒成立.
恒成立.
设![]() ,任取
,任取![]() ,且
,且![]()
则![]() ,
,
当![]() 且
且![]() 时,
时, ![]() ,
, ![]() ,
, ![]() ,
,
所以![]() ,所以
,所以![]() 在
在![]() 上是减函数;
上是减函数;
当![]() 且
且![]() 时,
时, ![]() ,
, ![]() ,
, ![]() ,
,
所以![]() ,所以
,所以![]() 在
在![]() 上是增函数,
上是增函数,
所以![]() ,即
,即![]() ,
,
所以![]() 的取值范围为
的取值范围为![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-4:坐标系与参数方程
在平面直角坐标系
 中,曲线
中,曲线 的参数方程为
的参数方程为 (
( ,
, 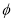 为参数),在以
为参数),在以 为极点,
为极点,  轴的正半轴为极轴的极坐标系中,曲线
轴的正半轴为极轴的极坐标系中,曲线 是圆心在极轴上,且经过极点的圆.已知曲线
是圆心在极轴上,且经过极点的圆.已知曲线 上的点
上的点 对应的参数
对应的参数 ,射线
,射线 与曲线
与曲线 交于点
交于点 .
.(Ⅰ)求曲线
 的直角坐标方程;
的直角坐标方程;(Ⅱ)若点
 ,
,  在曲线
在曲线 上,求
上,求 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】“共享单车”的出现,为我们提供了一种新型的交通方式.某机构为了调查人们对此种交通方式的满意度,从交通拥堵不严重的
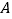 城市和交通拥堵严重的
城市和交通拥堵严重的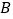 城市分别随机调查了20个用户,得到了一个用户满意度评分的样本,并绘制出茎叶图(如图所示):
城市分别随机调查了20个用户,得到了一个用户满意度评分的样本,并绘制出茎叶图(如图所示):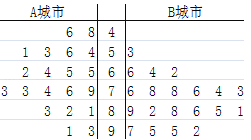
若得分不低于80分,则认为该用户对此种交通方式“认可”,否则认为该用户对此种交通方式“不认可”,请根据此样本完成此
 列联表,并据此样本分析是否有
列联表,并据此样本分析是否有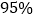 的把握认为城市拥堵与认可共享单车有关:
的把握认为城市拥堵与认可共享单车有关:
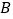
合计
认可
不认可
合计
附:参考数据:(参考公式:
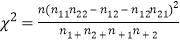 )
)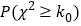
0.150
0.100
0.050
0.025
0.010
0.005
0.001

2.072
2.706
3.841
5.024
6.635
7.879
10.828
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知
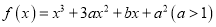 在
在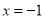 处的极值为0.
处的极值为0.(1)求常数
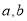 的值;
的值;(2)求
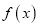 的单调区间;
的单调区间;(3)方程
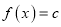 在区间
在区间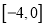 上有三个不同的实根时,求实数
上有三个不同的实根时,求实数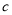 的范围.
的范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】在直角坐标系
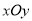 中,直线
中,直线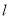 过点
过点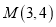 ,其倾斜角为
,其倾斜角为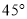 ,以原点为极点,以
,以原点为极点,以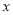 正半轴为极轴建立极坐标,并使得它与直角坐标系
正半轴为极轴建立极坐标,并使得它与直角坐标系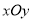 有相同的长度单位,圆
有相同的长度单位,圆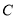 的极坐标方程为
的极坐标方程为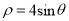 .
.(1)求直线
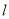 的参数方程和圆
的参数方程和圆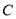 的普通方程;
的普通方程;(2)设圆
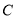 与直线
与直线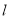 交于点
交于点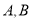 ,求
,求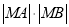 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】对于函数
 ,若在定义域内存在实数
,若在定义域内存在实数 ,满足
,满足 ,则称
,则称 为“局部奇函数”.
为“局部奇函数”.(1)已知二次函数
 ,试判断
,试判断 是否为“局部奇函数”?并说明理由;
是否为“局部奇函数”?并说明理由;(2)若
 是定义在区间
是定义在区间 上的“局部奇函数”,求实数
上的“局部奇函数”,求实数 的取值范围;
的取值范围;(3)若
 为定义域
为定义域 上的“局部奇函数”,求实数
上的“局部奇函数”,求实数 的取值范围;
的取值范围; -
科目: 来源: 题型:
查看答案和解析>>【题目】某厂生产某种产品的月固定成本为10(万元),每生产
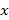 件,需另投入成本为
件,需另投入成本为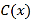 (万元).当月产量不足30件时,
(万元).当月产量不足30件时, 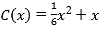 (万元);当月产量不低于30件时,
(万元);当月产量不低于30件时, 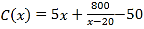 (万元).因设备问题,该厂月生产量不超过50件.现已知此商品每件售价为5万元,且该厂每个月生产的商品都能当月全部销售完.
(万元).因设备问题,该厂月生产量不超过50件.现已知此商品每件售价为5万元,且该厂每个月生产的商品都能当月全部销售完.(1)写出月利润
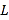 (万元)关于月产量
(万元)关于月产量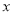 (件)的函数解析式;
(件)的函数解析式;(2)当月产量为多少件时,该厂所获月利润最大?
相关试题

