【题目】已知函数![]() (
(![]() ).
).
(1)当![]() 时,讨论
时,讨论![]() 的单调性;
的单调性;
(2)求![]() 在区间
在区间![]() 上的最小值.
上的最小值.
参考答案:
【答案】(1)![]() 的增区间为
的增区间为![]() ,
,![]() ,减区间为
,减区间为![]() ;(2)当
;(2)当![]() 时,
时,![]() 的最小值为
的最小值为![]() ;当
;当![]() 时,
时,![]() 的最小值为
的最小值为![]() ;当
;当![]() 时,
时,![]() 的最小值为
的最小值为![]() .
.
【解析】
试题分析:(1)研究单调性,可求出导函数![]() ,然后解不等式
,然后解不等式![]() 得单调增区间,解不等式
得单调增区间,解不等式![]() 得减区间,注意绝对值,要分类求解;(2)由于
得减区间,注意绝对值,要分类求解;(2)由于![]() ,因此先分类
,因此先分类![]() ,
,![]() ,
,![]() ,前两种情形,绝对值符号直接去掉,因此只要用导数
,前两种情形,绝对值符号直接去掉,因此只要用导数![]() 研究单调性可得最值,第三种情形同样要去绝对值符号,只是此时是分段函数,
研究单调性可得最值,第三种情形同样要去绝对值符号,只是此时是分段函数,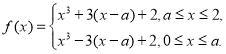 ,
,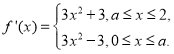 ,可以看出这时又要分类:
,可以看出这时又要分类:![]() ,
,![]() ,得单调性再得最小值.
,得单调性再得最小值.
试题解析:(1)当![]() 时,
时,![]() .
.
①当![]() 时,
时,![]() ,
,![]() ,
,
∴![]() 在
在![]() 单调递增;
单调递增;
②当![]() 时,
时,![]() ,
,![]() .
.
![]() 时,
时,![]() ,∴
,∴![]() 在
在![]() 单调递减;
单调递减;
![]() 时,
时,![]() ,∴
,∴![]() 在
在![]() 单调递增.
单调递增.
综上,![]() 的增区间为
的增区间为![]() ,
,![]() ,减区间为
,减区间为![]() .
.
(2)①![]() 时,
时,![]() ,
,![]() ,
,
![]() ,
,![]() .
.
②![]() 时,
时,![]() ,
,![]() ,
,
![]() ,
,![]() 在
在![]() 单调递增,
单调递增,
∴![]() .
.
③![]() 时,而
时,而![]() ,
,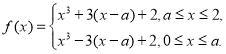
∴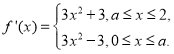
(i)![]() 时,
时,![]() 在
在![]() 上单增,
上单增,![]() 为最小值.
为最小值.
![]() 在
在![]() 上恒成立,
上恒成立,
∴![]() 在
在![]() 上单调递减,
上单调递减,
∴![]() .
.
(ii)![]() 时,
时,![]() 在
在![]() 上单调递增,
上单调递增,![]() .
.
在![]() 时,
时,![]() ,
,
∴![]() .
.
综上可知,当![]() 时,
时,![]() 的最小值为
的最小值为![]() ;当
;当![]() 时,
时,![]() 的最小值为
的最小值为![]() ;当
;当![]() 时,
时,![]() 的最小值为
的最小值为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在区间
 上,若函数
上,若函数 为增函数,而函数
为增函数,而函数 为减函数,则称函数
为减函数,则称函数 为区间
为区间 上的“弱增”函数.则下列函数中,在区间
上的“弱增”函数.则下列函数中,在区间 上不是“弱增”函数的为( )
上不是“弱增”函数的为( )A.
 B.
B. C.
C. D.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设函数
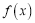 的定义域为D,如果
的定义域为D,如果 ,使得
,使得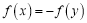 成立,则称函数
成立,则称函数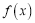 为“Ω函数”. 给出下列四个函数:①
为“Ω函数”. 给出下列四个函数:①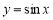 ;②
;②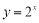 ;③
;③ ;④
;④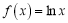 , 则其中“Ω函数”共有( )
, 则其中“Ω函数”共有( )A.1个 B.2个 C.3个 D.4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】根据统计资料,我国能源生产自1992年以来发展很快,下面是我国能源生产总量(折合亿吨标准煤)的几个统计数据:1992年8.6亿吨,5年后的1997年10.4亿吨,10年后的2002年12.9亿吨.有关专家预测,到2007年我国能源生产总量将达到17.1亿吨,则专家是依据下列哪一类函数作为数学模型进行预测的( )
A.一次函数 B.二次函数 C.指数函数 D.对数函数
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方体ABCD﹣A1B1C1D1的棱长为1,线段B1D1上有两个动点E,F,且EF=
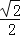 ,则下列结论中错误的是( )
,则下列结论中错误的是( )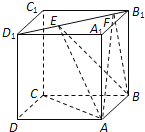
A.AC⊥BE
B.EF∥平面ABCD
C.三棱锥A﹣BEF的体积为定值
D.异面直线AE,BF所成的角为定值
-
科目: 来源: 题型:
查看答案和解析>>【题目】面数最少的棱柱为________棱柱,共有________个面围成.
-
科目: 来源: 题型:
查看答案和解析>>【题目】过P(4,-3)且在坐标轴上截距相等的直线有 ( )
A. 1条 B. 2条 C. 3条 D. 4条
相关试题

