【题目】a、b、c为三条不重合的直线,α、β、γ为三个不重合的平面,现给出六个命题.
①![]() a∥b; ②
a∥b; ②![]() a∥b; ③
a∥b; ③![]() α∥β;
α∥β;
④![]() α∥β; ⑤
α∥β; ⑤![]() a∥α; ⑥
a∥α; ⑥![]() a∥α,
a∥α,
其中正确的命题是________.(填序号)
参考答案:
【答案】①④
【解析】
在①中,由平行公理判断正误;在②中,a与b相交、平行或异面;在③中,α与β相交或平行;在④中,由面面平行的判定定理判断④的正误;在⑤中,a∥α,或aα;在⑥中,a∥α或aα.
由a,b,c为三条不重合的直线,α,β,γ为三个不重合的平面,知:
①∵a∥c,b∥c,∴由平行公理得a∥b,故①正确;
②∵a∥γ,b∥γ,∴a与b相交、平行或异面,故②错误;
③∵c∥α,c∥β,∴α与β相交或平行,故③错误;
④∵α∥γ,β∥γ,∴由面面平行的判定定理得α∥β,故④正确;
⑤∵c∥α,a∥c,∴a∥α,或aα,故⑤错误;
⑥∵a∥γ,![]() ,∴a∥α或aα,故⑥错误.
,∴a∥α或aα,故⑥错误.
故答案为:①④.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,ABCD与ADEF为平行四边形,M,N,G分别是AB,AD,EF的中点.求证:
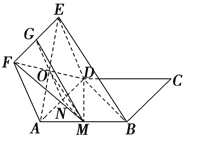
(1)BE∥平面DMF;
(2)平面BDE∥平面MNG.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知圆C:x2+y2+10x+10y+34=0.
(Ⅰ)试写出圆C的圆心坐标和半径;
(Ⅱ)圆D的圆心在直线x=-5上,且与圆C相外切,被x轴截得的弦长为10,求圆D的方程;
(Ⅲ)过点P(0,2)的直线交(Ⅱ)中圆D于E,F两点,求弦EF的中点M的轨迹方程.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四棱锥P-ABCD中,底面ABCD为菱形,∠BAD=60°,Q为AD的中点.
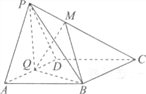
(Ⅰ)若PA=PD,求证:平面PQB⊥平面PAD;
(Ⅱ)点M在线段PC上,PM=tPC,试确定实数t的值,使PA∥平面MQB;
(Ⅲ)在(Ⅱ)的条件下,若平面PAD⊥平面ABCD,且PA=PD=AD=2,求二面角M-BQ-C的大小.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,已知圆O1与圆O2相交于A,B两点,过点A作圆O1的切线交圆O2于点C,过点B作两圆的割线,分别交圆O1 , 圆O2于点D,E,DE与AC相交于点P.
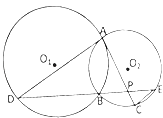
(1)求证:AD∥EC;
(2)若AD是圆O2的切线,且PA=3,PC=1,AD=6,求DB的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】在极坐标系中,已知曲线C1:ρ=2cosθ,将曲线C1上的点向左平移一个单位,然后纵坐标不变,横坐标伸长到原来的2倍,得到曲线C,又已知直线l:
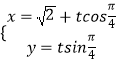 (t是参数),且直线l与曲线C交于A,B两点.
(t是参数),且直线l与曲线C交于A,B两点.
(1)求曲线C的直角坐标方程,并说明它是什么曲线;
(2)设定点P(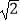 ,0),求|PA|+|PB|.
,0),求|PA|+|PB|. -
科目: 来源: 题型:
查看答案和解析>>【题目】设函数f(x)=
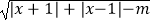 .
.
(1)当m=4时,求函数f(x)的定义域M;
(2)当a,b∈RM时,证明:2|a+b|<|4+ab|.
相关试题

