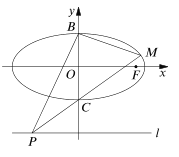
【题目】如图,已知椭圆![]() 的右焦点为
的右焦点为![]() ,点
,点![]() 分别是椭圆
分别是椭圆![]() 的上、下顶点,点
的上、下顶点,点![]() 是直线
是直线![]() 上的一个动点(与
上的一个动点(与![]() 轴的交点除外),直线
轴的交点除外),直线![]() 交椭圆于另一个点
交椭圆于另一个点![]() .
.
(1)当直线![]() 经过椭圆的右焦点
经过椭圆的右焦点![]() 时,求
时,求![]() 的面积;
的面积;
(2)①记直线![]() 的斜率分别为
的斜率分别为![]() ,求证:
,求证:![]() 为定值;
为定值;
②求![]() 的取值范围.
的取值范围.
参考答案:
【答案】(1)![]() (2)①见解析②
(2)①见解析②![]()
【解析】
试题(1)先联立直线![]() 的方程为
的方程为![]() 与椭圆方程
与椭圆方程![]() 的方程组,求出交点
的方程组,求出交点![]() 坐标
坐标![]() ,进而求出点到直线的距离公式求出上的高
,进而求出点到直线的距离公式求出上的高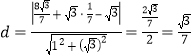 ,运用三角形的面积公式求解;(2)先求出斜率
,运用三角形的面积公式求解;(2)先求出斜率![]() 的值,再计算其积进行推算;先运用直线与椭圆的位置关系计算出向量的
的值,再计算其积进行推算;先运用直线与椭圆的位置关系计算出向量的![]() 的坐标形式,再运用向量的数量积公式进行推证:
的坐标形式,再运用向量的数量积公式进行推证:
解:(1)由题意![]() ,焦点
,焦点![]() ,
,
当直线![]() 过椭圆的右焦点
过椭圆的右焦点![]() 时,则直线
时,则直线![]() 的方程为
的方程为![]() ,即
,即![]() ,
,
联立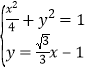 ,解得
,解得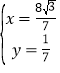 或
或![]() (舍),即
(舍),即![]() .
.
连![]() ,则直线
,则直线![]() ,即
,即 ![]() ,
,
而![]() ,
,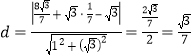 .
.
故![]() .
.
(2)解:法一:①设![]() ,且
,且![]() ,则直线
,则直线![]() 的斜率为
的斜率为![]() ,
,
则直线![]() 的方程为
的方程为![]() ,
,
联立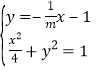 化简得
化简得![]() ,
,
解得![]() ,
,
所以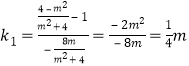 ,
,![]() ,
,
所以![]() 为定值.
为定值.
②由①知,![]() ,
,![]() ,
,
所以![]() ,
,
令![]()
故![]() ,
,
因为![]() 在
在![]() 上单调递增,
上单调递增,
所以![]() ,即
,即![]() 的取值范围为
的取值范围为![]() .
.
解法二:①设点![]() ,则直线
,则直线![]() 的方程为
的方程为![]() ,
,
令![]() ,得
,得![]() .
.
所以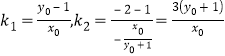 ,
,
所以![]() (定值).
(定值).
②由①知,![]() ,
,![]() ,
,
所以,![]()
![]() .
.
令![]() ,则
,则![]() ,
,
因为![]() 在
在![]() 上单调递减,
上单调递减,
所以![]() ,即
,即![]() 的取值范围为
的取值范围为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知正方形的中心为直线
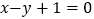 和直线
和直线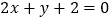 的交点,其一边所在直线方程为
的交点,其一边所在直线方程为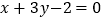
(1)写出正方形的中心坐标;
(2)求其它三边所在直线的方程(写出一般式).
-
科目: 来源: 题型:
查看答案和解析>>【题目】(12分)已知椭圆
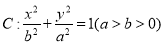 的离心率为
的离心率为 ,椭圆C的长轴长为4.
,椭圆C的长轴长为4.(1)求椭圆C的方程;
(2)已知直线
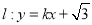 与椭圆C交于A,B两点,是否存在实数k使得以线段AB 为直径的圆恰好经过坐标原点O?若存在,求出k的值;若不存在,请说明理由.
与椭圆C交于A,B两点,是否存在实数k使得以线段AB 为直径的圆恰好经过坐标原点O?若存在,求出k的值;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=2
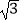 sin
sin 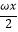 cos
cos 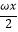 ﹣2sin2
﹣2sin2 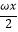 (ω>0)的最小正周期为3π.
(ω>0)的最小正周期为3π.
(I)求函数f(x)的单调递增区间;
(Ⅱ)在△ABC中,a,b,c分别为角A,B,C所对的边,a<b<c,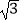 a=2csinA,并且f(
a=2csinA,并且f(  A+
A+  )=
)= 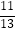 ,求cosB的值.
,求cosB的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知矩形
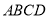 四点坐标为A(0,-2),C(4,2),B(4,-2),D(0,2).
四点坐标为A(0,-2),C(4,2),B(4,-2),D(0,2).
(1)求对角线
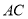 所在直线的方程;
所在直线的方程;(2)求矩形
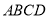 外接圆的方程;
外接圆的方程;(3)若动点
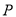 为外接圆上一点,点
为外接圆上一点,点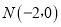 为定点,问线段PN中点的轨迹是什么,并求出该轨迹方程。
为定点,问线段PN中点的轨迹是什么,并求出该轨迹方程。 -
科目: 来源: 题型:
查看答案和解析>>【题目】连续抛掷同一颗均匀的骰子,令第i次得到的点数为ai , 若存在正整数k,使a1+a2+…+ak=6,则称k为你的幸运数字.
(1)求你的幸运数字为3的概率;
(2)若k=1,则你的得分为5分;若k=2,则你的得分为3分;若k=3,则你的得分为1分;若抛掷三次还没找到你的幸运数字则记0分,求得分X的分布列和数学期望. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知圆C的圆心在直线x﹣2y﹣3=0上,并且经过A(2,﹣3)和B(﹣2,﹣5),求圆C的标准方程.
相关试题

