【题目】已知A,B,C为锐角△ABC的三个内角,向量 ![]() =(2﹣2sinA,cosA+sinA),
=(2﹣2sinA,cosA+sinA), ![]() =(1+sinA,cosA﹣sinA),且
=(1+sinA,cosA﹣sinA),且 ![]() ⊥
⊥ ![]() .
.
(1)求A的大小;
(2)求y=2sin2B+cos( ![]() ﹣2B)取最大值时角B的大小.
﹣2B)取最大值时角B的大小.
参考答案:
【答案】
(1)解:∵ ![]() ,
,
∴(2﹣2sinA)(1+sinA)+(cosA+sinA)(cosA﹣sinA)=0
2(1﹣sin2A)=sin2A﹣cos2A
2cos2A=1﹣2cos2A
cos2A= ![]() .
.
∵△ABC是锐角三角形,∴cosA= ![]() A=
A= ![]() .
.
(2)解:∵△ABC是锐角三角形,且A= ![]() ,∴
,∴ ![]() <B<
<B< ![]()
∴ ![]()
=1﹣cos2B﹣ ![]() cos2B+
cos2B+ ![]() sin2B
sin2B
= ![]() sin2B﹣
sin2B﹣ ![]() cos2B+1
cos2B+1
= ![]() sin(2B﹣
sin(2B﹣ ![]() )+1
)+1
当y取最大值时,2B﹣ ![]() =
= ![]() ,即B=
,即B= ![]()
【解析】(1)根据两向量的垂直,利用两向量的坐标求得(2﹣2sinA)(1+sinA)+(cosA+sinA)(cosA﹣sinA)=0,利用同角三角函数的基本关系整理求得cosA的值,进而求得A.(2)根据A的值,求得B的范围,然后利用两角和公式和二倍角公式对函数解析式化简整理后.利用B的范围和正弦函数的单调性求得函数的最大值,及此时B的值.
【考点精析】掌握三角函数的最值是解答本题的根本,需要知道函数![]() ,当
,当![]() 时,取得最小值为
时,取得最小值为![]() ;当
;当![]() 时,取得最大值为
时,取得最大值为![]() ,则
,则![]() ,
,![]() ,
,![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】椭圆
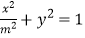 (m>1)与双曲线
(m>1)与双曲线 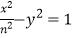 (n>0)有公共焦点F1 , F2 . P是两曲线的交点,则
(n>0)有公共焦点F1 , F2 . P是两曲线的交点,则 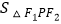 =( )
=( )
A.4
B.2
C.1
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
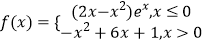 ,g(x)=f(x)+m,若函数g(x)恰有三个不同零点,则实数m的取值范围为( )
,g(x)=f(x)+m,若函数g(x)恰有三个不同零点,则实数m的取值范围为( )
A.(1,10)
B.(﹣10,﹣1)
C.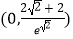
D.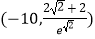
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知数列{an}的首项
 ,
,  ,n=1,2,3,….
,n=1,2,3,….
(1)证明:数列 是等比数列;
是等比数列;
(2)数列 的前n项和Sn .
的前n项和Sn . -
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙、丙三人参加了一家公司的招聘面试,面试合格者可正式签约,甲表示只要面试合格就签约.乙、丙则约定:两人面试都合格就一同签约,否则两人都不签约.设每人面试合格的概率都是
 ,且面试是否合格互不影响.求:
,且面试是否合格互不影响.求:
(1)至少有1人面试合格的概率;
(2)签约人数ξ的分布列和数学期望. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
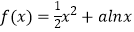 .
.
(1)当a<0时,若x>0,使f(x)≤0成立,求a的取值范围;
(2)令g(x)=f(x)﹣(a+1)x,a∈(1,e],证明:对x1 , x2∈[1,a],恒有|g(x1)﹣g(x2)|<1. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆E的中心在坐标原点,焦点在x轴上,离心率为
 ,且椭圆E上一点到两个焦点距离之和为4;l1 , l2是过点P(0,2)且互相垂直的两条直线,l1交E于A,B两点,l2交E交C,D两点,AB,CD的中点分别为M,N.
,且椭圆E上一点到两个焦点距离之和为4;l1 , l2是过点P(0,2)且互相垂直的两条直线,l1交E于A,B两点,l2交E交C,D两点,AB,CD的中点分别为M,N.
(1)求椭圆E的方程;
(2)求l1的斜率k的取值范围;
(3)求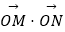 的取值范围.
的取值范围.
相关试题

