【题目】某地4个蔬菜大棚顶部,阳光照在一棵棵茁壮生长的蔬菜上.这些采用水培、无土栽培方式种植的各类蔬菜,成为该地区居民争相购买的对象.过去50周的资料显示,该地周光照量![]() (小时)都在30以上.其中不足50的周数大约有5周,不低于50且不超过70的周数大约有35周,超过70的大约有10周.根据统计某种改良黄瓜每个蔬菜大棚增加量
(小时)都在30以上.其中不足50的周数大约有5周,不低于50且不超过70的周数大约有35周,超过70的大约有10周.根据统计某种改良黄瓜每个蔬菜大棚增加量![]() (百斤)与每个蔬菜大棚使用农夫1号液体肥料
(百斤)与每个蔬菜大棚使用农夫1号液体肥料![]() (千克)之间对应数据为如图所示的折线图:
(千克)之间对应数据为如图所示的折线图:
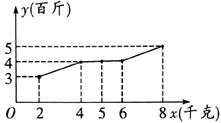
(Ⅰ)依据数据的折线图,用最小二乘法求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;并根据所求线性回归方程,估计如果每个蔬菜大棚使用农夫1号肥料10千克,则这种改良黄瓜每个蔬菜大棚增加量
;并根据所求线性回归方程,估计如果每个蔬菜大棚使用农夫1号肥料10千克,则这种改良黄瓜每个蔬菜大棚增加量![]() 是多少斤?
是多少斤?
(Ⅱ)因蔬菜大棚对光照要求较大,某光照控制仪商家为应对恶劣天气对光照的影响,为该基地提供了部分光照控制仪,该商家希望安装的光照控制仪尽可能运行,但每周光照控制仪最多可运行台数受周光照量![]() 限制,并有如下关系:
限制,并有如下关系:
周光照量 |
|
|
|
光照控制仪最多可运行台数 | 3 | 2 | 1 |
若某台光照控制仪运行,则该台光照控制仪周利润为5000元;若某台光照控制仪未运行,则该台光照控制仪周亏损800元,欲使商家周总利润的均值达到最大,应安装光照控制仪多少台?
附:回归方程系数公式: 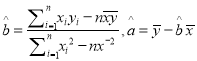 .
.
参考答案:
【答案】(1) ![]() ;(2)
;(2)![]() .
.
【解析】试题分析:(Ⅰ)算出样本中心点的坐标,利用公式求得![]() ,由
,由![]() 可得
可得![]() ,即可得回归方程,再将
,即可得回归方程,再将![]() 时代入即可得结果;(Ⅱ)分别求出安装2台光照控制仪的周利润的均值、安装3台光照控制仪的均值,与安装1台光照控制仪可获得周利润进行比较即可得结果.
时代入即可得结果;(Ⅱ)分别求出安装2台光照控制仪的周利润的均值、安装3台光照控制仪的均值,与安装1台光照控制仪可获得周利润进行比较即可得结果.
试题解析:(Ⅰ) ![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
,
所以![]() 关于
关于![]() 的线性回归方程为
的线性回归方程为![]() ,
,
当![]() 时,
时, ![]() 百斤=550斤,
百斤=550斤,
所以估计如果每个蔬菜大棚使用农夫1号肥料10千克,则这种改良黄瓜每个蔬菜大棚增加量![]() 是500斤.
是500斤.
(Ⅱ)记商家总利润为![]() 元,由已知条件可知至少需安装1台,
元,由已知条件可知至少需安装1台,
①安装1台光照控制仪可获得周利润5000元,
②安装2台光照控制仪的情形:
当![]() 时,一台光照控制仪运行,此时
时,一台光照控制仪运行,此时![]() 元,
元,
当![]() 时,两台光照控制仪都运行,此时
时,两台光照控制仪都运行,此时![]() 元,
元,
故![]() 的分布列为
的分布列为
| 4200 | 10000 |
| 0.2 | 0.8 |
所以![]() 元,
元,
③安装3台光照控制仪的情形:
当![]() 时,一台光照控制仪运行,此时
时,一台光照控制仪运行,此时![]() 元,
元,
当![]() 时,两台光照控制仪运行,此时
时,两台光照控制仪运行,此时![]() 元,
元,
当![]() 时,三台光照控制仪都运行,此时
时,三台光照控制仪都运行,此时![]() 元,
元,
故![]() 的分布列为
的分布列为
| 3400 | 9200 | 15000 |
| 0.2 | 0.7 | 0.1 |
所以![]() 元,
元,
综上,为使商家周总利润的均值达到最大应该安装2台光照控制仪.
【方法点晴】本题主要考查线性回归方程及离散型随机变量的分布列与数学期望,属于难题.求回归直线方程的步骤:①依据样本数据确定两个变量具有线性相关关系;②计算![]() 的值;③计算回归系数
的值;③计算回归系数![]() ;④写出回归直线方程为
;④写出回归直线方程为![]() ;(2) 回归直线过样本点中心
;(2) 回归直线过样本点中心![]() 是一条重要性质,利用线性回归方程可以估计总体,帮助我们分析两个变量的变化趋势.
是一条重要性质,利用线性回归方程可以估计总体,帮助我们分析两个变量的变化趋势.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直三棱柱
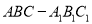 中,
中, 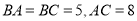 ,
, 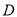 为线段
为线段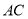 的中点.
的中点.(Ⅰ)求证:
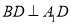 ;
;(Ⅱ)若直线
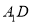 与平面
与平面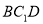 所成角的正弦值为
所成角的正弦值为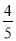 ,求
,求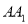 的长.
的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知△ABC的内角A,B,C的对边分别为a,b,c,且b=acosc+
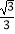 csinA.
csinA.
(1)求角A的大小;
(2)当a=3时,求△ABC周长的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知
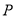 是抛物线
是抛物线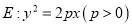 上一点,
上一点,  到直线
到直线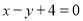 的距离为
的距离为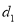 ,
, 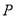 到
到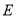 的准线的距离为
的准线的距离为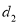 ,且
,且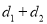 的最小值为
的最小值为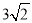 .
.(Ⅰ)求抛物线
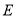 的方程;
的方程;(Ⅱ)直线
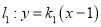 交
交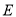 于点
于点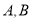 ,直线
,直线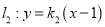 交
交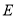 于点
于点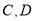 ,线段
,线段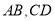 的中点分别为
的中点分别为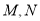 ,若
,若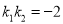 ,直线
,直线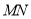 的斜率为
的斜率为 ,求证:直线
,求证:直线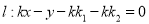 恒过定点.
恒过定点. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 (
(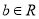 ,
, 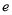 为自然对数的底数)在点
为自然对数的底数)在点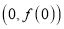 处的切线经过点
处的切线经过点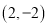 .
.(Ⅰ)讨论函数
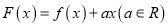 的单调性;
的单调性;(Ⅱ)若
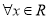 ,不等式
,不等式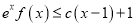 恒成立,求实数
恒成立,求实数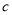 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知数列{an}的各项均为正数,前n和为Sn , 且Sn=
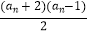 (n∈N*).
(n∈N*).
(1)求证:数列{an}是等差数列;
(2)设bn=an3n , 求数列{bn}的前n项的和Tn . -
科目: 来源: 题型:
查看答案和解析>>【题目】已知平面向量
 ,
,  (
(  ≠
≠  )满足
)满足 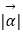 =2,且
=2,且  与
与  ﹣
﹣  的夹角为120° , t∈R,则|(1﹣t)
的夹角为120° , t∈R,则|(1﹣t)  +t
+t  |的最小值是 . 已知
|的最小值是 . 已知 
 =0,向量
=0,向量  满足(
满足(  ﹣
﹣  )(
)(  ﹣
﹣  )=0,|
)=0,|  ﹣
﹣  |=5,|
|=5,|  ﹣
﹣  |=3,则
|=3,则 
 的最大值为 .
的最大值为 .
相关试题

