Question

【题目】在如图所示的空间几何体中，平面ACD⊥平面ABC，△ACD与△ACB是边长为2的等边三角形，BE=2，BE和平面ABC所成的角为60°，且点E在平面ABC上的射影落在的平分线上.

（1）求证：DE∥平面ABC；

（2）求此空间几何体的体积.

Answer 1

【答案】（1）详见解析；（2）.

【解析】

试题分析：（1）要证明线面平行，即先证明线线平行，取AC中点O，连接BO，DO，则BO⊥AC，DO⊥AC，作EF⊥平面ABC，根据题意，点F落在BO上，∴EBF=60°，易求得，这样就可证明,且,所以四边形是平行四边形，得到;（2）将几何体的体积分割为两个三棱锥的体积，即,根据所给的数据代入得到结果.

试题解析：（1）由题意知，△ABC，△ACD都是边长为2的等边三角形，取AC中点O，连接BO，DO，则BO⊥AC，DO⊥AC，

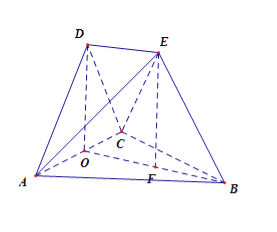
又∵平面ACD⊥平面ABC，∴DO⊥平面ABC，作EF⊥平面ABC，那么EF∥DO，根据题意，点F落在BO上，∴EBF=60°，易求得，

∴四边形DEFO是平行四边形，∴DE∥OF，DE平面ABC，OF平面ABC，

∴DE∥平面ABC.

（2）由（1）：BO⊥AC，平面ACD⊥平面ABC且交线为AC，

∴BO⊥平面ACD，∴DE⊥平面ACD，

∴三棱锥E-ACD的体积

，

三棱锥E-ACB的体积，

∴此空间几何体的体积.