【题目】对于每项均是正整数的数列A:a1,a2,…,an,定义变换T1,T1将数列A变换成数列T1(A):n,a1-1,a2-1,…,an-1.对于每项均是非负整数的数列B:b1,b2,…,bm,定义变换T2,T2将数列B各项从大到小排列,然后去掉所有为零的项,得到数列T2(B).又定义S(B)=2(b1+2b2+…+mbm)+![]() +
+![]() +…+
+…+![]() .设A0是每项均为正整数的有穷数列,令Ak+1=T2(T1(Ak))(k=0,1,2,…).
.设A0是每项均为正整数的有穷数列,令Ak+1=T2(T1(Ak))(k=0,1,2,…).
(1)如果数列A0为2,6,4,8,写出数列A1,A2;
(2)对于每项均是正整数的有穷数列A,证明:S(T1(A))=S(A);
(3)证明:对于任意给定的每项均为正整数的有穷数列A0,存在正整数K,当k≥K时,S(Ak+1)=S(Ak).
参考答案:
【答案】(1)A1:7,5,4,3,1;A2:6,5,4,3,2.(2)见解析(3)见解析
【解析】试题分析:(1)由A0:2,6,4,8,求得T1(A0),再通过![]() 求解。(2)设有穷数列A,求得T1(A),再求得S(T1(A)),两者作差比较。(3)设A是每项均为非负整数的数列a1,a2,…,
求解。(2)设有穷数列A,求得T1(A),再求得S(T1(A)),两者作差比较。(3)设A是每项均为非负整数的数列a1,a2,…,![]() ,在存在1≤i<j≤n,使得
,在存在1≤i<j≤n,使得![]() 时,交换数列A的第i项与第j项得到数列B,,在存在1≤m<n,使得am+1=am+2=an=0条件下,若记数列a1,a2,…
时,交换数列A的第i项与第j项得到数列B,,在存在1≤m<n,使得am+1=am+2=an=0条件下,若记数列a1,a2,…![]() 为C,
为C,
Ak+1=T2(T1(Ak)), S(Ak+1)≤S(T1(Ak)),由S(T1(Ak))=S(Ak),得到S(Ak+1)≤S(Ak),S(Ak)是大于2的整数,所以经过有限步后,必有S(Ak)=S(Ak+1)=S(Ak+2)=0.
试题解析: (1) A0:2,6,4,8;T1(A0):4,1,5,3,7,A1:7,5,4,3,1;T1(A1):5,6,4,3,2,0,
∴A2:6,5,4,3,2.
(2)证明 设每项均是正整数的有穷数列A为a1,a2,…,![]()
则T1(A)为n,a1-1,a2-1,…,![]() -1,
-1,
从而S(T1(A))=2[n+2(a1-1)+3(a2-1)+…+(n+1)(![]() -1)]+n2+(a1-1)2+(a2-1)2+…+(
-1)]+n2+(a1-1)2+(a2-1)2+…+(![]() -1)2.
-1)2.
又S(A)=2(a1+2a2+…+nan)+![]() +
+![]() +…+
+…+![]() ,
,
所以S(T1(A))-S(A)=2[n-2-3-…-(n+1)]+2(a1+a2+…+an)+n2-2(a1+a2+…+![]() )
)
+n=-n(n+1)+n2+n=0,
故S(T1(A))=S(A).
(3)证明:设A是每项均为非负整数的数列a1,a2,…,![]()
当存在1≤i<j≤n,使得![]() 时,交换数列A的第i项与第j项得到数列B,
时,交换数列A的第i项与第j项得到数列B,
则S(B)-S(A)=![]()
当存在1≤m<n,使得am+1=am+2=an=0时,若记数列a1,a2,…![]() 为C,
为C,
则S(C)=S(A).
所以S(T2(A))≤S(A).
从而对于任意给定的数列A0,由Ak+1=T2(T1(Ak))(k=0,1,2),
可知S(Ak+1)≤S(T1(Ak)).
又由(2)可知S(T1(Ak))=S(Ak),
所以S(Ak+1)≤S(Ak).
即对于k∈N,要么有S(Ak+1)=S(Ak),
要么有S(Ak+1)≤S(Ak)-1.
因为S(Ak)是大于2的整数,所以经过有限步后,
必有S(Ak)=S(Ak+1)=S(Ak+2)=0.
即存在正整数K,当k≥K时,S(Ak+1)=S(A).
-
科目: 来源: 题型:
查看答案和解析>>【题目】设f(x)、g(x)、h(x)是定义域为R的三个函数,对于命题:①f(x)+g(x)、f(x)+h(x)、g(x)+h(x)均为增函数,则f(x)、g(x)、h(x)中至少有一个增函数;②若f(x)+g(x)、f(x)+h(x)、g(x)+h(x)均是以T为周期的函数,则f(x)、g(x)、h(x)均是以T为周期的函数,下列判断正确的是( )
A.①和②均为真命题
B.①和②均为假命题
C.①为真命题,②为假命题
D.①为假命题,②为真命题 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正三棱柱ABC-A1B1C1,底面△ABC的边长AB=1,侧棱长为
 ,P是A1B1的中点,E、F、G分别是AC,BC,PC的中点.
,P是A1B1的中点,E、F、G分别是AC,BC,PC的中点.
(1)求FG与BB1所成角的大小;
(2)求证:平面EFG∥平面ABB1A1.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设a>0,b>0,若关于x,y的方程组
 无解,则a+b的取值范围为 .
无解,则a+b的取值范围为 . -
科目: 来源: 题型:
查看答案和解析>>【题目】设a,b∈R,c∈[0,2π),若对于任意实数x都有2sin(3x﹣
 )=asin(bx+c),则满足条件的有序实数组(a,b,c)的组数为 .
)=asin(bx+c),则满足条件的有序实数组(a,b,c)的组数为 . -
科目: 来源: 题型:
查看答案和解析>>【题目】设an=1+
 +=
+= +…+
+…+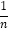 (n∈N*),是否存在一次函数g(x),使得a1+a2+a3+…+an-1=g(n)(an-1)对n≥2的一切正整数都成立?并试用数学归纳法证明你的结论.
(n∈N*),是否存在一次函数g(x),使得a1+a2+a3+…+an-1=g(n)(an-1)对n≥2的一切正整数都成立?并试用数学归纳法证明你的结论. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD是圆柱OO′的轴截面,点P在圆柱OO′的底面圆周上,圆柱OO′的底面圆的半径OA=1,侧面积为2π,∠AOP=60°.

(1)求证:PB⊥平面APD;
(2)是否存在点G在PD上,使得AG⊥BD;并说明理由.
(3)求三棱锥D-AGB的体积.
相关试题

