【题目】设f(x)、g(x)、h(x)是定义域为R的三个函数,对于命题:①f(x)+g(x)、f(x)+h(x)、g(x)+h(x)均为增函数,则f(x)、g(x)、h(x)中至少有一个增函数;②若f(x)+g(x)、f(x)+h(x)、g(x)+h(x)均是以T为周期的函数,则f(x)、g(x)、h(x)均是以T为周期的函数,下列判断正确的是( )
A.①和②均为真命题
B.①和②均为假命题
C.①为真命题,②为假命题
D.①为假命题,②为真命题
参考答案:
【答案】D
【解析】解:①不成立.可举反例:f(x)=![]() .g(x)=
.g(x)=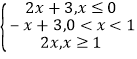 ,h(x)=
,h(x)=![]() .
.
②∵f(x)+g(x)=f(x+T)+g(x+T),f(x)+h(x)=f(x+T)+h(x+T),h(x)+g(x)=h(x+T)+g(x+T),
前两式作差可得:g(x)﹣h(x)=g(x+T)﹣h(x+T),结合第三式可得:g(x)=g(x+T),h(x)=h(x+T),同理可得:f(x)=f(x+T),因此②正确.
故选:D.
①不成立.可举反例:f(x)= ![]() .g(x)=
.g(x)= 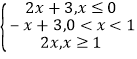 ,h(x)=
,h(x)= ![]() .
.
②由题意可得:f(x)+g(x)=f(x+T)+g(x+T),f(x)+h(x)=f(x+T)+h(x+T),h(x)+g(x)=h(x+T)+g(x+T),
可得:g(x)=g(x+T),h(x)=h(x+T),f(x)=f(x+T),即可判断出真假.;本题考查了函数的单调性与周期性、简易逻辑的判定方法,考查了推理能力与计算能力,属于中档题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 .
.(1)判断f(x)的奇偶性,说明理由;
(2)当x>0时,判断f(x)的单调性并加以证明;
(3)若f(2t)-mf(t)>0对于t∈(0,+∞)恒成立,求m的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法中,正确的是______(填上所有符合条件的序号)
①y=e-x在R上为增函数
②任取x>0,均有3x>2x
③函数y=f(x)的图象与直线x=a可能有两个交点
④y=2|x|的最小值为1;
⑤与y=3x的图象关于直线y=x对称的函数为y=log3x.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=x2+2
 ax+3a+2.
ax+3a+2.(1)若函数f(x)的值域为[0,+∞),求a的值;
(2)若函数f(x)的函数值均为非负实数,求g(a)=2-a|a+3|的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正三棱柱ABC-A1B1C1,底面△ABC的边长AB=1,侧棱长为
 ,P是A1B1的中点,E、F、G分别是AC,BC,PC的中点.
,P是A1B1的中点,E、F、G分别是AC,BC,PC的中点.
(1)求FG与BB1所成角的大小;
(2)求证:平面EFG∥平面ABB1A1.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设a>0,b>0,若关于x,y的方程组
 无解,则a+b的取值范围为 .
无解,则a+b的取值范围为 . -
科目: 来源: 题型:
查看答案和解析>>【题目】对于每项均是正整数的数列A:a1,a2,…,an,定义变换T1,T1将数列A变换成数列T1(A):n,a1-1,a2-1,…,an-1.对于每项均是非负整数的数列B:b1,b2,…,bm,定义变换T2,T2将数列B各项从大到小排列,然后去掉所有为零的项,得到数列T2(B).又定义S(B)=2(b1+2b2+…+mbm)+
 +
+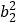 +…+
+…+ .设A0是每项均为正整数的有穷数列,令Ak+1=T2(T1(Ak))(k=0,1,2,…).
.设A0是每项均为正整数的有穷数列,令Ak+1=T2(T1(Ak))(k=0,1,2,…).(1)如果数列A0为2,6,4,8,写出数列A1,A2;
(2)对于每项均是正整数的有穷数列A,证明:S(T1(A))=S(A);
(3)证明:对于任意给定的每项均为正整数的有穷数列A0,存在正整数K,当k≥K时,S(Ak+1)=S(Ak).
相关试题

