【题目】设甲、乙、丙三个乒乓球协会的分别选派3,1,2名运动员参加某次比赛,甲协会运动员编号分别为A1 , A2 , A3 , 乙协会编号为A4 , 丙协会编号分别为A5 , A6 , 若从这6名运动员中随机抽取2名参加双打比赛.
(1)用所给编号列出所有可能抽取的结果;
(2)求丙协会至少有一名运动员参加双打比赛的概率;
(3)求参加双打比赛的两名运动员来自同一协会的概率.
参考答案:
【答案】
(1)解:从这6名运动员中随机抽取2名参加双打比赛,
所有可能的结果为{A1,A2},{A1,A3},{A1,A4},{A1,A5},{A1,A6},
{A2,A3},{A2,A4},{A2,A5},{A2,A6},{A3,A4},{A3,A5},
{A3,A6},{A4,A5},{A4,A6},{A5,A6},共15种
(2)解:∵丙协会至少有一名运动员参加双打比赛,
∴编号为A5,A6的两名运动员至少有一人被抽到,
其结果为:{A1,A5},{A1,A6},{A2,A5},{A2,A6},{A3,A5},
{A3,A6},{A4,A5},{A4,A6},{A5,A6},共9种,
∴丙协会至少有一名运动员参加双打比赛的概率P(A)= ![]()
(3)解:两名运动员来自同一协会有{A1,A2},{A1,A3},{A2,A3},{A5,A6}共4种
参加双打比赛的两名运动员来自同一协会的概率为 ![]()
【解析】(1)从这6名运动员中随机抽取2名参加双打比赛,利用列举法能求出所有可能的结果.(2)由丙协会至少有一名运动员参加双打比赛,知编号为A5 , A6的两名运动员至少有一人被抽到,由此利用列举法能求出丙协会至少有一名运动员参加双打比赛的概率.(3)由列举法得两名运动员来自同一协会有4种,由此能求出参加双打比赛的两名运动员来自同一协会的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,AC平分∠DAB,∠ABC=60°,AC=6,AD=5,S△ADC=
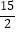 ,求AB的长.
,求AB的长. 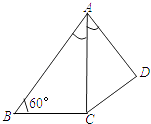
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是计算1+
 +
+ 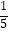 +…+
+…+  的值的一个程序框图,其中判断框内应填的是( )
的值的一个程序框图,其中判断框内应填的是( ) 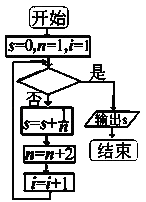
A.i>10
B.i<10
C.i>20
D.i<20 -
科目: 来源: 题型:
查看答案和解析>>【题目】某纺纱厂生产甲、乙两种棉纱,已知生产甲种棉纱1吨需耗一级籽棉2吨、二级籽棉1吨;生产乙种棉纱1吨需耗一级籽棉1吨,二级籽棉2吨.每1吨甲种棉纱的利润为900元,每1吨乙种棉纱的利润为600元.工厂在生产这两种棉纱的计划中,要求消耗一级籽棉不超过250吨,二级籽棉不超过300吨.问甲、乙两种棉纱应各生产多少吨,能使利润总额最大?并求出利润总额的最大值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在四棱锥P﹣ABCD中,PD⊥平面ABCD,底面是边长是1的正方形,侧棱PA与底面成45°的角,M,N,分别是AB,PC的中点;
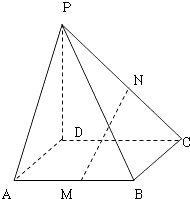
(1)求证:MN∥平面PAD;
(2)求四棱锥P﹣ABCD的体积. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知集合
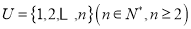 ,对于集合
,对于集合 的两个非空子集
的两个非空子集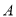 ,
, 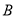 ,若
,若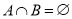 ,则称
,则称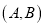 为集合
为集合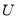 的一组“互斥子集”.记集合
的一组“互斥子集”.记集合 的所有“互斥子集”的组数为
的所有“互斥子集”的组数为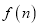 (视
(视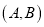 与
与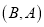 为同一组“互斥子集”).
为同一组“互斥子集”).(1)写出
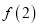 ,
,  ,
, 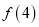 的值;
的值;(2)求
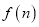 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-4:坐标系与参数方程
在直角坐标系
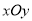 中,曲线
中,曲线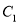 :
: 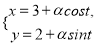 (
(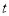 为参数,
为参数, 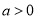 ),在以坐标原点为极点,
),在以坐标原点为极点, 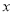 轴的非负半轴为极轴的极坐标系中,曲线
轴的非负半轴为极轴的极坐标系中,曲线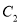 :
: 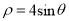 .
.(1)试将曲线
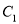 与
与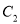 化为直角坐标系
化为直角坐标系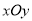 中的普通方程,并指出两曲线有公共点时
中的普通方程,并指出两曲线有公共点时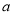 的取值范围;
的取值范围;(2)当
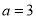 时,两曲线相交于
时,两曲线相交于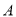 ,
, 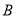 两点,求
两点,求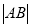 .
.
相关试题

