搜索
【题目】有13名医生，其中女医生6人，现从中抽调5名医生组成医疗小组前往灾区，若医疗小组至少有2名男医生，同时至多有3名女医生，设不同的选派方法种数为N，则下列等式：
①C135﹣C71C64；②C72C63+C73C62+C74C61+C75；
③C135﹣C71C64﹣C65； ④C72C113；
其中能成为N的算式是______．
参考答案：
【答案】②③
【解析】13名医生，其中女医生6人，男医生7人。
利用直接法,2男3女： 
6;3男2女： 
;4男1女： 
;5男： 
,所以N= C72C63+C73C62+C74C61+C75；
利用间接法：13名医生,任取5人,减去4、5名女医生的情况,
即N= C135﹣C71C64﹣C65；
所以能成为N的算式是②③.
-
科目： 来源： 题型：
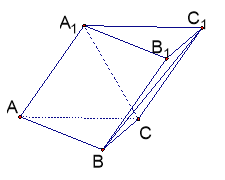
查看答案和解析>>【题目】如图，三棱柱
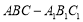中，侧面
，
，
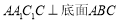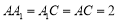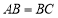且
.
（Ⅰ）求证：
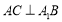；（Ⅱ）求二面角
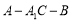的余弦值. -
科目： 来源： 题型：
查看答案和解析>>【题目】已知甲、乙、丙、丁、戊、己等6人.（以下问题用数字作答）
（1）邀请这6人去参加一项活动，必须有人去，去几人自行决定，共有多少种不同的情形？
（2）这6人同时加入6项不同的活动，每项活动限1人，其中甲不参加第一项活动，乙不参加第三项活动，共有多少种不同的安排方法？
（3）将这6人作为辅导员安排到3项不同的活动中，每项活动至少安排1名辅导员；求丁、戊、己恰好被安排在同一项活动中的概率．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知
.（Ⅰ）证明：
；（Ⅱ）证明：当
时，
. -
科目： 来源： 题型：
查看答案和解析>>【题目】已知函数
，
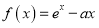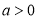.（Ⅰ）记
的极小值为
，求
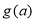的最大值；（Ⅱ）若对任意实数
恒有
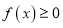，求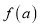
的取值范围. -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在四棱锥
中，
为正三角形，
,
,
,
平面
.
（Ⅰ）点
在棱
上，试确定点的位置，使得
平面
;（Ⅱ）求二面角
的余弦值. -
科目： 来源： 题型：
查看答案和解析>>【题目】在人群流量较大的街道，有一中年人吆喝“送钱”，只见他手拿一黑色小布袋，袋中有3只黄色、3只白色的乒乓球（其体积、质地完成相同），旁边立着一块小黑板写道：
摸球方法：从袋中随机摸出3个球，若摸得同一颜色的3个球，摊主送给摸球者5元钱；若摸得非同一颜色的3个球，摸球者付给摊主1元钱．
（1）摸出的3个球为白球的概率是多少？
（2）摸出的3个球为2个黄球1个白球的概率是多少？
（3）假定一天中有100人次摸奖，试从概率的角度估算一下这个摊主一个月（按30天计）能赚多少钱？
相关试题
