【题目】如图,在四棱锥![]() 中,
中,![]() 为正三角形,
为正三角形,![]() ,
,![]() ,
,![]() ,
,![]() 平面
平面![]() .
.

(Ⅰ)点![]() 在棱
在棱![]() 上,试确定点
上,试确定点![]() 的位置,使得
的位置,使得![]() 平面
平面![]() ;
;
(Ⅱ)求二面角![]() 的余弦值.
的余弦值.
参考答案:
【答案】(Ⅰ)当![]() 为
为![]() 中点时
中点时![]() .(Ⅱ)二面角
.(Ⅱ)二面角![]() 的余弦值为
的余弦值为![]() .
.
【解析】
试题分析:(Ⅰ)根据题意,以![]() 为坐标原点,射线
为坐标原点,射线![]() ,
,![]() ,
,![]() 分别为
分别为![]() ,
,![]() ,
,![]() 轴的正方向建立空间直角坐标系,设
轴的正方向建立空间直角坐标系,设![]() ,若
,若![]() ,则
,则![]() ,即
,即![]() ,在空间直角坐标系中求出相应向量坐标,可求出
,在空间直角坐标系中求出相应向量坐标,可求出![]() ,由此确定点
,由此确定点![]() 的位置(Ⅱ)在空间直角坐标系中求出平面
的位置(Ⅱ)在空间直角坐标系中求出平面![]() 的一个法向量
的一个法向量![]() ,再求出平面
,再求出平面![]() 的一个法向量
的一个法向量![]() ,利用夹角公式即可求得二面角
,利用夹角公式即可求得二面角![]() 的余弦值.
的余弦值.
试题解析:
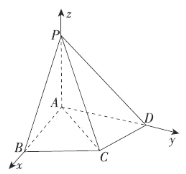
(Ⅰ)∵![]() ∴
∴![]() ;又∵
;又∵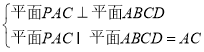 ,∴
,∴![]() ,可得
,可得![]() ,
,![]() ,以
,以![]() 为坐标原点,射线
为坐标原点,射线![]() ,
,![]() ,
,![]() 分别为
分别为![]() ,
,![]() ,
,![]() 轴的正方向建立空间直角坐标系,设
轴的正方向建立空间直角坐标系,设![]() ,则
,则![]() ,
,![]() ,
,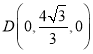 ,
,![]() .
.
(Ⅰ)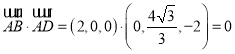 ,故
,故![]() ;
;
设![]() ,若
,若![]() ,则
,则![]() ,即
,即![]() ,
,
即![]() ,即
,即![]() ,即当
,即当![]() 为
为![]() 中点时,
中点时,![]() ,
,
则![]() .所以当
.所以当![]() 为
为![]() 中点时
中点时![]() .
.
(Ⅱ)设平面![]() 的一个法向量
的一个法向量![]() ,
,
![]() ,
,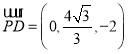 ,则
,则![]() 且
且![]() ,
,
即![]() 且
且![]() ,
,
令![]() ,则
,则![]() ,
,![]() ,则
,则![]() ,
,
再取平面![]() 的一个法向量
的一个法向量![]() .
.
则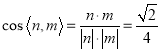 ,
,
故二面角![]() 的余弦值为
的余弦值为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知
 .
.(Ⅰ)证明:
 ;
;(Ⅱ)证明:当
 时,
时, .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】有13名医生,其中女医生6人,现从中抽调5名医生组成医疗小组前往灾区,若医疗小组至少有2名男医生,同时至多有3名女医生,设不同的选派方法种数为N,则下列等式:
①C135﹣C71C64;②C72C63+C73C62+C74C61+C75;
③C135﹣C71C64﹣C65; ④C72C113;
其中能成为N的算式是______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
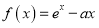 ,
,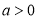 .
.(Ⅰ)记
 的极小值为
的极小值为 ,求
,求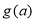 的最大值;
的最大值;(Ⅱ)若对任意实数
 恒有
恒有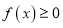 ,求
,求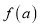 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】在人群流量较大的街道,有一中年人吆喝“送钱”,只见他手拿一黑色小布袋,袋中有3只黄色、3只白色的乒乓球(其体积、质地完成相同),旁边立着一块小黑板写道:
摸球方法:从袋中随机摸出3个球,若摸得同一颜色的3个球,摊主送给摸球者5元钱;若摸得非同一颜色的3个球,摸球者付给摊主1元钱.
(1)摸出的3个球为白球的概率是多少?
(2)摸出的3个球为2个黄球1个白球的概率是多少?
(3)假定一天中有100人次摸奖,试从概率的角度估算一下这个摊主一个月(按30天计)能赚多少钱?
-
科目: 来源: 题型:
查看答案和解析>>【题目】在如图所示的直三棱柱
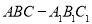 中,
中,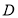 ,
,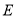 分别是
分别是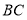 ,
,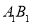 的中点.
的中点.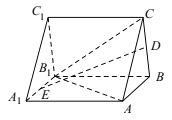
(Ⅰ)求证:
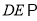 平面
平面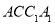 ;
;(Ⅱ)若
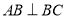 ,
,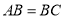 ,
, ,求直线
,求直线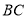 与平面
与平面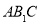 所成角的正切值.
所成角的正切值. -
科目: 来源: 题型:
查看答案和解析>>【题目】设
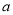 、
、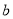 是两条不同直线,
是两条不同直线, 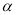 、
、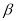 是两个不同平面,则下列四个命题:
是两个不同平面,则下列四个命题:① 若
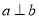 ,
, 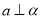 ,
, 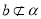 ,则
,则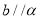 ;
;② 若
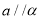 ,
, 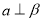 ,则
,则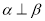 ;
;③ 若
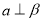 ,
, 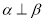 ,则
,则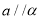 或
或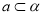 ;
;④ 若
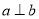 ,
, 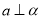 ,
, 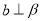 ,则
,则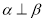 .
. 其中正确命题的个数为 ( )
A. 1 B. 2 C. 3 D. 4
相关试题

