【题目】如图,三棱柱![]() 中,侧面
中,侧面![]() ,
,![]() ,
,![]() 且
且![]() .
.
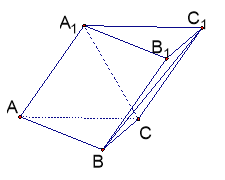
(Ⅰ)求证:![]() ;
;
(Ⅱ)求二面角![]() 的余弦值.
的余弦值.
参考答案:
【答案】(Ⅰ)见解析;(Ⅱ)![]() .
.
【解析】
试题分析:作![]() 的中点
的中点![]() ,因为
,因为![]() ,且
,且![]() 为
为![]() 的中点可得
的中点可得![]() ,又侧面
,又侧面![]() 底面
底面![]() ,由此可证
,由此可证![]() 底面
底面![]() ,以
,以![]() 为坐标原点,
为坐标原点,![]() 、
、![]() 、
、![]() 所在直线分别为
所在直线分别为![]() 轴建立空间直角坐标系.(Ⅰ)写出相应点的坐标,求出
轴建立空间直角坐标系.(Ⅰ)写出相应点的坐标,求出![]() 与
与![]() ,由
,由![]() 可证
可证![]() ;(Ⅱ)求出平面
;(Ⅱ)求出平面![]() 的法向量与平面
的法向量与平面![]() 的法向量,由向量知识求即可.
的法向量,由向量知识求即可.
试题解析:(Ⅰ)作![]() 的中点
的中点![]() ,因为
,因为![]() ,且
,且![]() 为
为![]() 的中点,
的中点,
∴![]() ,
,
又侧面![]() ,其交线为
,其交线为![]() ,且
,且![]() ,
,
∴![]() (2分)
(2分)
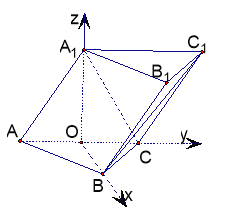
以![]() 为坐标原点,
为坐标原点,![]() 、
、![]() 、
、![]() 所在直线分别为
所在直线分别为![]() 轴建立空间直角坐标系:
轴建立空间直角坐标系:
由已知得:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,则有:
,则有:![]() ,
,![]() ,
,![]() ,
,
∴![]() (6分)
(6分)
(Ⅱ)由(Ⅰ)得可设平面![]() 的法向量为
的法向量为![]() ,同理平面
,同理平面![]() 的法向量为
的法向量为![]() ,
,
则满足: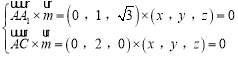
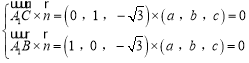 ,
,
解得:![]() ,
,![]() ,
,
则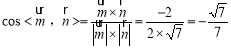 .
.
∴二面角![]() 的余弦值为
的余弦值为![]() . (12分)
. (12分)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB为圆O的直径,点E,F在圆O上,且AB//EF,AB=2EF,矩形ABCD所在的平面和圆O所在的平面互相垂直.
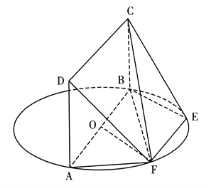
(I)证明:OF//平面BEC;
(Ⅱ)证明:平面ADF
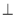 平面BCF.
平面BCF. -
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两位射击运动员,在某天训练中已各射击10次,每次命中的环数如下:
甲 7 8 7 9 5 4 9 10 7 4
乙 9 5 7 8 7 6 8 6 7 7
(Ⅰ)通过计算估计,甲、乙二人的射击成绩谁更稳;
(Ⅱ)若规定命中8环及以上环数为优秀,以频率作为概率,请依据上述数据估计,求甲在第11至第13次射击中获得优秀的次数
 的分布列和期望.
的分布列和期望. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
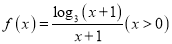 的图象上有一点列
的图象上有一点列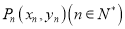 ,点
,点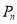 在
在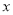 轴上的射影是
轴上的射影是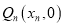 ,且
,且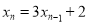 (
(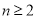 且
且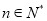 ),
),  .
.(1)求证:
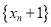 是等比数列,并求出数列
是等比数列,并求出数列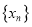 的通项公式;
的通项公式;(2)对任意的正整数
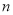 ,当
,当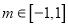 时,不等式
时,不等式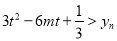 恒成立,求实数
恒成立,求实数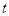 的取值范围.
的取值范围.(3)设四边形
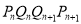 的面积是
的面积是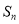 ,求证:
,求证: 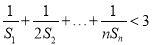 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知甲、乙、丙、丁、戊、己等6人.(以下问题用数字作答)
(1)邀请这6人去参加一项活动,必须有人去,去几人自行决定,共有多少种不同的情形?
(2)这6人同时加入6项不同的活动,每项活动限1人,其中甲不参加第一项活动,乙不参加第三项活动,共有多少种不同的安排方法?
(3)将这6人作为辅导员安排到3项不同的活动中,每项活动至少安排1名辅导员;求丁、戊、己恰好被安排在同一项活动中的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知
 .
.(Ⅰ)证明:
 ;
;(Ⅱ)证明:当
 时,
时, .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】有13名医生,其中女医生6人,现从中抽调5名医生组成医疗小组前往灾区,若医疗小组至少有2名男医生,同时至多有3名女医生,设不同的选派方法种数为N,则下列等式:
①C135﹣C71C64;②C72C63+C73C62+C74C61+C75;
③C135﹣C71C64﹣C65; ④C72C113;
其中能成为N的算式是______.
相关试题

