【题目】已知![]() 是直线
是直线![]() 上任意一点,过
上任意一点,过![]() 作
作![]() ,线段
,线段![]() 的垂直平分线交
的垂直平分线交![]() 于点
于点![]() .
.
(Ⅰ)求点![]() 的轨迹
的轨迹![]() 对应的方程;
对应的方程;
(Ⅱ)过点![]() 的直线
的直线![]() 与点
与点![]() 的轨迹
的轨迹![]() 相交于
相交于![]() 两点,(
两点,( ![]() 点在
点在![]() 轴上方),点
轴上方),点![]() 关于
关于![]() 轴的对称点为
轴的对称点为![]() ,且
,且![]() ,求
,求![]() 的外接圆的方程.
的外接圆的方程.
参考答案:
【答案】(1)![]() (2)
(2)![]()
【解析】试题分析:(Ⅰ)本问考查轨迹方程的求法,根据题画出图形辅助分析,观察图形可知,恒有![]() ,根据定义到定点
,根据定义到定点![]() 与定直线
与定直线![]() 距离相等的点轨迹为抛物线,因此点
距离相等的点轨迹为抛物线,因此点![]() 的轨迹是以
的轨迹是以![]() 为焦点,以
为焦点,以![]() 为准线的抛物线,可以求出相应的方程为
为准线的抛物线,可以求出相应的方程为![]() ;(Ⅱ)本问重点考查直线与抛物线问题,分析题意可知,过点
;(Ⅱ)本问重点考查直线与抛物线问题,分析题意可知,过点![]() 的直线
的直线![]() 斜率显然存在且不为0,所以可设直线
斜率显然存在且不为0,所以可设直线![]() 的方程为
的方程为![]() ,联立直线
,联立直线![]() 方程与抛物线
方程与抛物线![]() 方程,消去未知数
方程,消去未知数![]() ,得到关于
,得到关于![]() 的一元二次方程,需要考虑到的条件有判别式
的一元二次方程,需要考虑到的条件有判别式![]() ,韦达定理,然后根据
,韦达定理,然后根据![]() ,转化为
,转化为![]() ,通过坐标表示,于是可以求出
,通过坐标表示,于是可以求出![]() 的值,这样就得到了直线
的值,这样就得到了直线![]() 的方程,接下来需要确定
的方程,接下来需要确定![]() 的外接圆圆心和半径,线段
的外接圆圆心和半径,线段![]() ,
, ![]() 垂直平分线的交点即为圆心,在根据弦长公式确定半径即可,于是得到外接圆方程.
垂直平分线的交点即为圆心,在根据弦长公式确定半径即可,于是得到外接圆方程.
试题解析:(Ⅰ)连接![]() ,由于
,由于![]() 是线段
是线段![]() 垂直平分线上的点,则
垂直平分线上的点,则![]() ,即
,即![]() 到点
到点![]() 的距离和到直线
的距离和到直线![]() 的距离相等、所以点
的距离相等、所以点![]() 的轨迹是以
的轨迹是以![]() 为焦点,
为焦点, ![]() 为准线的抛物线.
为准线的抛物线.
其中![]()
所以点![]() 的轨迹
的轨迹![]() 对应的方程为
对应的方程为![]() .
.
(Ⅱ)设![]() ,
, ![]() ,
, ![]() ,
, ![]() 的方程为
的方程为![]() .
.
将![]() 代入
代入![]() 并整理得
并整理得
![]() ,由
,由![]() ,
,
从而![]() ,
, ![]() ,
,
![]() ,
, ![]() .
.
因为![]() ,
,
故![]() ,解得
,解得![]() ,
,
所以![]() 的方程为
的方程为![]() ,
,
设![]() 中点为
中点为![]() ,
,
则![]() ,
, ![]() ,
,
![]() 中垂线方程
中垂线方程![]() .
.
令![]() 得
得![]() ,圆心坐标
,圆心坐标![]() ,到
,到![]() 的距离为
的距离为![]() .
.
![]() ,
,
所以圆的半径![]()
![]() 的外接圆
的外接圆![]() 的方程
的方程![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为迎接2017年“双
 ”,“双
”,“双 ”购物狂欢节的来临,某青花瓷生产厂家计划每天生产汤碗、花瓶、茶杯这三种瓷器共
”购物狂欢节的来临,某青花瓷生产厂家计划每天生产汤碗、花瓶、茶杯这三种瓷器共 个,生产一个汤碗需
个,生产一个汤碗需 分钟,生产一个花瓶需
分钟,生产一个花瓶需 分钟,生产一个茶杯需
分钟,生产一个茶杯需 分钟,已知总生产时间不超过
分钟,已知总生产时间不超过 小时.若生产一个汤碗可获利润
小时.若生产一个汤碗可获利润 元,生产一个花瓶可获利润
元,生产一个花瓶可获利润 元,生产一个茶杯可获利润
元,生产一个茶杯可获利润 元.
元.(1)使用每天生产的汤碗个数
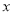 与花瓶个数
与花瓶个数 表示每天的利润
表示每天的利润 (元);
(元);(2)怎样分配生产任务才能使每天的利润最大,最大利润是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】设函数f(x)=
 , 若对任意给定的t∈(1,+∞),都存在唯一的x∈R,满足f(f(x))=2at2+at,则正实数a的最小值是( )
, 若对任意给定的t∈(1,+∞),都存在唯一的x∈R,满足f(f(x))=2at2+at,则正实数a的最小值是( )
A.1
B.
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在如图所示的多面体中,
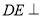 平面
平面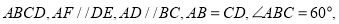
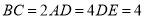 .
.
(Ⅰ)在
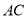 上求作
上求作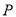 ,使
,使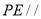 平面
平面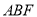 ,请写出作法并说明理由;
,请写出作法并说明理由;(Ⅱ)若
 在平面
在平面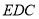 的正投影为
的正投影为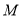 ,求四面体
,求四面体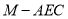 的体积.
的体积. -
科目: 来源: 题型:
查看答案和解析>>【题目】某车间计划每天生产卡车模型、赛车模型、小汽车模型这三种玩具共100个,已知生产一个卡车模型需5分钟,生产一个赛车模型需7分钟,生产一个小汽车模型需4分钟,且生产一个卡车模型可获利润8元,生产一个赛车模型可获利润9元,生产一个小汽车模型可获利润6元.若总生产时间不超过10小时,该公司合理分配生产任务使每天的利润最大,则最大利润是______________元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知公差大于零的等差数列
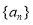 的前
的前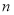 项和为
项和为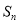 ,且
,且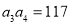 ,
,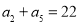 .
.(1)求数列
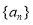 的通项公式;
的通项公式;(2)若数列
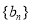 是等差数列,且
是等差数列,且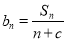 ,求非零常数
,求非零常数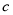 的值.
的值.(3)设
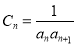 ,
,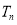 为数列
为数列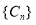 的前
的前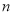 项和,是否存在正整数
项和,是否存在正整数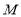 ,使得
,使得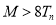 对任意的
对任意的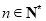 均成立?若存在,求出
均成立?若存在,求出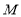 的最小值;若不存在,请说明理由.
的最小值;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
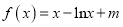 若曲线
若曲线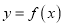 在
在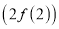 处的切线方程为
处的切线方程为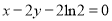 .
.(Ⅰ)求
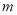 的值;
的值;(Ⅱ)若对于任意
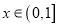 ,总有
,总有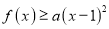 ,求实数
,求实数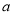 的取值范围.
的取值范围.
相关试题

