【题目】设函数f(x)=![]() , 若对任意给定的t∈(1,+∞),都存在唯一的x∈R,满足f(f(x))=2at2+at,则正实数a的最小值是( )
, 若对任意给定的t∈(1,+∞),都存在唯一的x∈R,满足f(f(x))=2at2+at,则正实数a的最小值是( )
A.1
B.![]()
C.![]()
D.![]()
参考答案:
【答案】C
【解析】解:∵f(x)=![]() ,
,
∴当x≤0时,
f(f(x))=![]() =x;
=x;
当0<x≤1时,log2x≤0;
故f(f(x))=![]() =x;
=x;
当x>1时,
f(f(x))=log2(log2x);
故f(f(x))=![]() ;
;
分析函数在各段上的取值范围可知,
若对任意给定的t∈(1,+∞),都存在唯一的x∈R,满足f(f(x))=2at2+at,
则f(f(x))>1,
即2at2+at>1,
又∵t∈(1,+∞),a>0;
∴2a+a≥1即可,
即a≥![]() ;
;
故选:C.
【考点精析】利用函数的最值及其几何意义对题目进行判断即可得到答案,需要熟知利用二次函数的性质(配方法)求函数的最大(小)值;利用图象求函数的最大(小)值;利用函数单调性的判断函数的最大(小)值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为选拔选手参加“中国谜语大会”,某中学举行了一次“谜语大赛”活动.为了了解本次竞赛学生的成绩情况,从中抽取了部分学生的分数(得分取正整数,满分为100分)作为样本(样本容量为
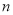 )进行统计.按照
)进行统计.按照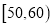 ,
, 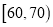 ,
, 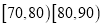 ,
, 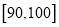 的分组作出频率分布直方图,并作出样本分数的茎叶图(图中仅列出了得分在
的分组作出频率分布直方图,并作出样本分数的茎叶图(图中仅列出了得分在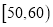 ,
, 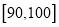 的数据).
的数据).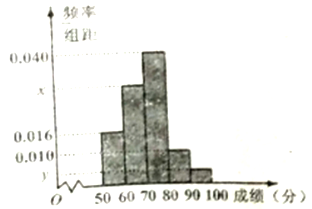

(Ⅰ)求样本容量
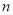 和频率分布直方图中的
和频率分布直方图中的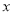 ,
, 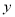 的值;
的值;(Ⅱ)分数在
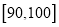 的学生设为一等奖,获奖学金500元;分数在
的学生设为一等奖,获奖学金500元;分数在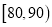 的学生设为二等奖,获奖学金200元.已知在样本中,获一、二等奖的学生中各有一名男生,则从剩下的女生中任取三人,求奖学金之和大于600的概率.
的学生设为二等奖,获奖学金200元.已知在样本中,获一、二等奖的学生中各有一名男生,则从剩下的女生中任取三人,求奖学金之和大于600的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-4:坐标系与参数方程
在直角坐标系
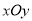 中,直线
中,直线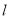 的方程为
的方程为 ,曲线
,曲线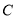 的参数方程为
的参数方程为 (
(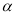 为参数).
为参数).(1)已知在极坐标系(与直角坐标系
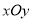 取相同的长度单位,且以原点
取相同的长度单位,且以原点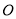 为极点,以
为极点,以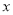 轴正半轴为极轴)中,点
轴正半轴为极轴)中,点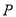 的极坐标为
的极坐标为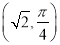 ,判断点
,判断点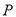 与曲线
与曲线 的位置关系;
的位置关系;(2)设点
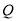 是曲线
是曲线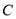 上的一个动点,求它到直线
上的一个动点,求它到直线 的距离的最小值.
的距离的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】为迎接2017年“双
 ”,“双
”,“双 ”购物狂欢节的来临,某青花瓷生产厂家计划每天生产汤碗、花瓶、茶杯这三种瓷器共
”购物狂欢节的来临,某青花瓷生产厂家计划每天生产汤碗、花瓶、茶杯这三种瓷器共 个,生产一个汤碗需
个,生产一个汤碗需 分钟,生产一个花瓶需
分钟,生产一个花瓶需 分钟,生产一个茶杯需
分钟,生产一个茶杯需 分钟,已知总生产时间不超过
分钟,已知总生产时间不超过 小时.若生产一个汤碗可获利润
小时.若生产一个汤碗可获利润 元,生产一个花瓶可获利润
元,生产一个花瓶可获利润 元,生产一个茶杯可获利润
元,生产一个茶杯可获利润 元.
元.(1)使用每天生产的汤碗个数
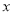 与花瓶个数
与花瓶个数 表示每天的利润
表示每天的利润 (元);
(元);(2)怎样分配生产任务才能使每天的利润最大,最大利润是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】在如图所示的多面体中,
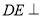 平面
平面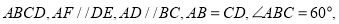
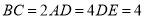 .
.
(Ⅰ)在
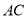 上求作
上求作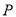 ,使
,使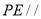 平面
平面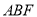 ,请写出作法并说明理由;
,请写出作法并说明理由;(Ⅱ)若
 在平面
在平面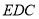 的正投影为
的正投影为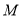 ,求四面体
,求四面体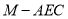 的体积.
的体积. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知
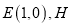 是直线
是直线 上任意一点,过
上任意一点,过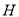 作
作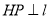 ,线段
,线段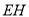 的垂直平分线交
的垂直平分线交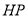 于点
于点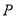 .
.(Ⅰ)求点
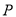 的轨迹
的轨迹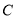 对应的方程;
对应的方程;(Ⅱ)过点
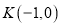 的直线
的直线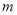 与点
与点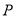 的轨迹
的轨迹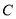 相交于
相交于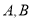 两点,(
两点,( 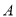 点在
点在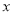 轴上方),点
轴上方),点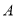 关于
关于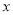 轴的对称点为
轴的对称点为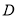 ,且
,且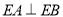 ,求
,求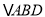 的外接圆的方程.
的外接圆的方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】某车间计划每天生产卡车模型、赛车模型、小汽车模型这三种玩具共100个,已知生产一个卡车模型需5分钟,生产一个赛车模型需7分钟,生产一个小汽车模型需4分钟,且生产一个卡车模型可获利润8元,生产一个赛车模型可获利润9元,生产一个小汽车模型可获利润6元.若总生产时间不超过10小时,该公司合理分配生产任务使每天的利润最大,则最大利润是______________元.
相关试题

