【题目】已知函数![]() 若曲线
若曲线![]() 在
在![]() 处的切线方程为
处的切线方程为![]() .
.
(Ⅰ)求![]() 的值;
的值;
(Ⅱ)若对于任意![]() ,总有
,总有![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
参考答案:
【答案】(1)![]() (2)
(2)![]()
【解析】试题分析:(Ⅰ)本问考查导数的几何意义,根据曲线在点![]() 处切线方程为
处切线方程为![]() ,当
,当![]() 时,代入计算得出
时,代入计算得出![]() ,即
,即![]() ,根据函数
,根据函数![]() ,则
,则![]() ,所以
,所以![]() ,另外本题也可以求出点
,另外本题也可以求出点![]() 处的切线方程,再根据题中的方程,就可以确定
处的切线方程,再根据题中的方程,就可以确定![]() 的值;(Ⅱ)对于任意
的值;(Ⅱ)对于任意![]() ,
, ![]() 恒成立,等价转化为对于任意
恒成立,等价转化为对于任意![]() ,
, ![]() 恒成立,设函数
恒成立,设函数![]() ,则问题转化为只需满足
,则问题转化为只需满足![]() ,接下来对
,接下来对![]() 求导,
求导, ![]() ,对
,对![]() 分类讨论,在
分类讨论,在![]() 的取值范围不同时,分别求函数
的取值范围不同时,分别求函数![]() 在区间
在区间![]() 上的最小值,满足
上的最小值,满足![]() ,于是得到
,于是得到![]() 的取值范围.
的取值范围.
试题解析:(Ⅰ) ![]() ,
,
则![]() ,
,
又因为切点为![]() ,
,
所以切线方程为![]() ,
,
即: ![]() ,
,
所以![]() ,
,
即![]() .
.
(Ⅱ)设![]() ,则
,则![]() 在
在![]() 上恒成立.
上恒成立.
![]() ,
,
若![]() ,则
,则![]() 在
在![]() 上恒成立,
上恒成立, ![]() 在
在![]() 上单调递减,
上单调递减,
![]() ,
,
所以![]() 符合题意.
符合题意.
若![]() ,则
,则![]() ,
,
令![]() ,得
,得![]() 或
或![]() ,
,
若![]() 则
则![]() , 则
, 则![]() ,在
,在![]() 上恒成立,
上恒成立, ![]() 在
在![]() 上单调递减,
上单调递减,
![]() 所以
所以![]() 符合题意.
符合题意.
若![]() ,则
,则![]() ,
,
当![]() 时,
时, ![]() 单调递减;当
单调递减;当![]() 时,
时, ![]() 单调递增.
单调递增.
这时![]() ,不符合题意.
,不符合题意.
若![]() ,则
,则![]() ,则
,则![]() 在
在![]() 上恒成立,
上恒成立, ![]() 在
在![]() 上单调递减,
上单调递减,
![]() 所以
所以![]() 符合题意.
符合题意.
综上所述: ![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知
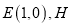 是直线
是直线 上任意一点,过
上任意一点,过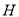 作
作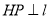 ,线段
,线段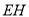 的垂直平分线交
的垂直平分线交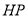 于点
于点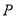 .
.(Ⅰ)求点
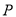 的轨迹
的轨迹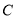 对应的方程;
对应的方程;(Ⅱ)过点
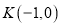 的直线
的直线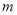 与点
与点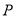 的轨迹
的轨迹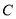 相交于
相交于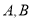 两点,(
两点,( 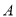 点在
点在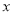 轴上方),点
轴上方),点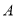 关于
关于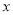 轴的对称点为
轴的对称点为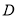 ,且
,且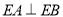 ,求
,求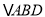 的外接圆的方程.
的外接圆的方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】某车间计划每天生产卡车模型、赛车模型、小汽车模型这三种玩具共100个,已知生产一个卡车模型需5分钟,生产一个赛车模型需7分钟,生产一个小汽车模型需4分钟,且生产一个卡车模型可获利润8元,生产一个赛车模型可获利润9元,生产一个小汽车模型可获利润6元.若总生产时间不超过10小时,该公司合理分配生产任务使每天的利润最大,则最大利润是______________元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知公差大于零的等差数列
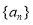 的前
的前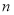 项和为
项和为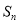 ,且
,且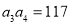 ,
,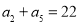 .
.(1)求数列
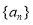 的通项公式;
的通项公式;(2)若数列
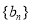 是等差数列,且
是等差数列,且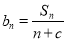 ,求非零常数
,求非零常数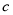 的值.
的值.(3)设
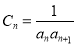 ,
,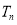 为数列
为数列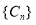 的前
的前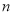 项和,是否存在正整数
项和,是否存在正整数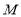 ,使得
,使得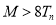 对任意的
对任意的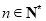 均成立?若存在,求出
均成立?若存在,求出 的最小值;若不存在,请说明理由.
的最小值;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列五个命题中:
①函数y=loga(2x﹣1)+2015(a>0且a≠1)的图象过定点(1,2015);
②若定义域为R函数f(x)满足:对任意互不相等的x1、x2都有(x1﹣x2)[f(x1)﹣f(x2)]>0,则f(x)是减函数;
③f(x+1)=x2﹣1,则f(x)=x2﹣2x;
④若函数f(x)= 是奇函数,则实数a=﹣1;
是奇函数,则实数a=﹣1;
⑤若a= (c>0,c≠1),则实数a=3.
(c>0,c≠1),则实数a=3.
其中正确的命题是 .(填上相应的序号). -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD是平行四边形,平面AED⊥平面ABCD,EF∥AB,AB=2,BC=EF=1,AE=
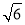 ,DE=3,∠BAD=60,G为BC的中点.
,DE=3,∠BAD=60,G为BC的中点.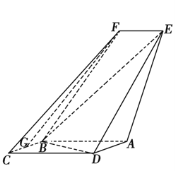
(1)求证:FG
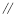 平面BED;
平面BED;(2)求证:平面BED⊥平面AED;
(3)求直线EF与平面BED所成角的正弦值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=
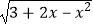 的定义域为A,集合B={x|(x﹣m﹣3)(x﹣m+3)≤0}.
的定义域为A,集合B={x|(x﹣m﹣3)(x﹣m+3)≤0}.
(1)求A和f(x)的值域C;
(2)若A∩B=[2,3],求实数m的值;
(3)若CRB,求实数m的取值范围.
相关试题

