【题目】给出下列四个命题:
①回归直线![]() 过样本点中心(
过样本点中心(![]() ,
,![]() )
)
②将一组数据中的每个数据都加上或减去同一个常数后,平均值不变
③将一组数据中的每个数据都加上或减去同一个常数后,方差不变
④在回归方程![]() =4x+4中,变量x每增加一个单位时,y平均增加4个单位
=4x+4中,变量x每增加一个单位时,y平均增加4个单位
其中错误命题的序号是( )
A.①B.②C.③D.④
参考答案:
【答案】B
【解析】
由回归直线都过样本中心,可判断①;由均值和方差的性质可判断②③;由回归直线方程的特点可判断④,得到答案.
对于①中,回归直线![]() 过样本点中心
过样本点中心![]() ,故①正确;
,故①正确;
对于②中,将一组数据中的每个数据都加上或减去同一个常数后,平均值为加上或减去这个常数,故②错误;
对于③中,将一组数据中的每个数据都加上或减去同一个常数后,方差不变,故③正确;
对于④中,在回归直线方程![]() ,变量
,变量![]() 每增加一个单位时,
每增加一个单位时,![]() 平均增加4个单位,故④正确,
平均增加4个单位,故④正确,
故选B.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系
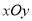 中,曲线
中,曲线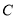 的参数方程为
的参数方程为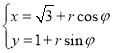 (
(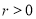 ,
,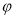 为参数),以坐标原点
为参数),以坐标原点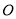 为极点,
为极点,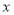 轴正半轴为极轴建立极坐标系,直线
轴正半轴为极轴建立极坐标系,直线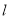 的极坐标方程为
的极坐标方程为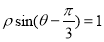 ,若直线
,若直线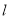 与曲线
与曲线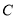 相切;
相切; (1)求曲线
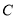 的极坐标方程与直线
的极坐标方程与直线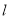 的直角坐标方程;
的直角坐标方程;(2)在曲线
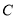 上取两点
上取两点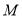 ,
,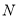 与原点
与原点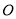 构成
构成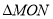 ,且满足
,且满足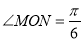 ,求
,求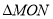 面积的最大值.
面积的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】2018年央视大型文化节目《经典咏流传》的热播,在全民中掀起了诵读诗词的热潮.某大学社团调查了该校文学院300名学生每天诵读诗词的时间(所有学生诵读时间都在两小时内),并按时间(单位:分钟)将学生分成六个组:
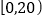 ,
, ,
,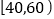 ,
,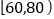 ,
,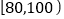 ,
, ,经统计得到了如图所
,经统计得到了如图所示的频率分布直方图
(Ⅰ)求频率分布直方图中
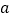 的值,并估计该校文学院的学生每天诵读诗词的时间的平均数;
的值,并估计该校文学院的学生每天诵读诗词的时间的平均数;(Ⅱ)若两个同学诵读诗词的时间
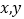 满足
满足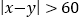 ,则这两个同学组成一个“Team”,已知从每天诵读时间小于20分钟和大于或等于80分钟的所有学生中用分层抽样的方法抽取了5人,现从这5人中随机选取2人,求选取的两人能组成一个“Team”的概率.
,则这两个同学组成一个“Team”,已知从每天诵读时间小于20分钟和大于或等于80分钟的所有学生中用分层抽样的方法抽取了5人,现从这5人中随机选取2人,求选取的两人能组成一个“Team”的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
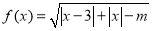 的定义域为
的定义域为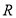 ;
;(1)求实数
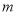 的取值范围;
的取值范围;(2)设实数
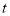 为
为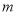 的最大值,若实数
的最大值,若实数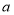 ,
,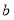 ,
,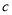 满足
满足 ,求
,求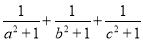 的最小值.
的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】某公司计划购买1台机器,该种机器使用三年后即被淘汰.机器有一易损零件,在购进机器时,可以额外购买这种零件作为备件,每个200元.在机器使用期间,如果备件不足再购买,则每个500元.现需决策在购买机器时应同时购买几个易损零件,为此搜集并整理了100台这种机器在三年使用期内更换的易损零件数,得下面柱状图:

记x表示1台机器在三年使用期内需更换的易损零件数,y表示1台机器在购买易损零件上所需的费用(单位:元),
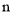 表示购机的同时购买的易损零件数.
表示购机的同时购买的易损零件数.(Ⅰ)若
 =19,求y与x的函数解析式;
=19,求y与x的函数解析式;(Ⅱ)若要求“需更换的易损零件数不大于
 ”的频率不小于0.5,求
”的频率不小于0.5,求 的最小值;
的最小值;(Ⅲ)假设这100台机器在购机的同时每台都购买19个易损零件,或每台都购买20个易损零件,分别计算这100台机器在购买易损零件上所需费用的平均数,以此作为决策依据,购买1台机器的同时应购买19个还是20个易损零件?
-
科目: 来源: 题型:
查看答案和解析>>【题目】“绿水青山就是金山银山”,为了保护环境,减少空气污染,某空气净化器制造厂,决定投入生产某种惠民型的空气净化器.根据以往的生产销售经验得到年生产销售的统计规律如下:①年固定生产成本为2万元;②每生产该型号空气净化器1百台,成本增加1万元;③年生产x百台的销售收入
 (万元).假定生产的该型号空气净化器都能卖出(利润=销售收入﹣生产成本).
(万元).假定生产的该型号空气净化器都能卖出(利润=销售收入﹣生产成本).(1)为使该产品的生产不亏本,年产量x应控制在什么范围内?
(2)该产品生产多少台时,可使年利润最大?
-
科目: 来源: 题型:
查看答案和解析>>【题目】《中华人民共和国道路交通安全法》第47条的相关规定:机动车行经人行横道时,应当减速慢行;遇行人正在通过人行横道,应当停车让行,俗称“礼让斑马线”,《中华人民共和国道路交通安全法》 第90条规定:对不礼让行人的驾驶员处以扣3分,罚款50元的处罚.下表是某市一主干路口监控设备所抓拍的5个月内驾驶员不“礼让斑马线”行为统计数据:
月份
1
2
3
4
5
违章驾驶员人数
120
105
100
90
85
(1)请利用所给数据求违章人数y与月份之间的回归直线方程
 +
+
(2)预测该路口7月份的不“礼让斑马线”违章驾驶员人数;
(3)交警从这5个月内通过该路口的驾驶员中随机抽查了50人,调查驾驶员不“礼让斑马线”行为与驾龄的关系,得到如下2
 列联表:
列联表:不礼让斑马线
礼让斑马线
合计
驾龄不超过1年
22
8
30
驾龄1年以上
8
12
20
合计
30
20
50
能否据此判断有97.5
 的把握认为“礼让斑马线”行为与驾龄有关?
的把握认为“礼让斑马线”行为与驾龄有关?参考公式及数据:
 ,
, .
.
0.150
0.100
0.050
0.025
0.010
0.005
0.001
k
2.072
2.706
3.841
5.024
6.635
7.879
10.828
 (其中n=a+b+c+d)
(其中n=a+b+c+d)
相关试题

