【题目】2018年央视大型文化节目《经典咏流传》的热播,在全民中掀起了诵读诗词的热潮.某大学社团调查了该校文学院300名学生每天诵读诗词的时间(所有学生诵读时间都在两小时内),并按时间(单位:分钟)将学生分成六个组:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,经统计得到了如图所
,经统计得到了如图所
示的频率分布直方图
(Ⅰ)求频率分布直方图中![]() 的值,并估计该校文学院的学生每天诵读诗词的时间的平均数;
的值,并估计该校文学院的学生每天诵读诗词的时间的平均数;
(Ⅱ)若两个同学诵读诗词的时间![]() 满足
满足![]() ,则这两个同学组成一个“Team”,已知从每天诵读时间小于20分钟和大于或等于80分钟的所有学生中用分层抽样的方法抽取了5人,现从这5人中随机选取2人,求选取的两人能组成一个“Team”的概率.
,则这两个同学组成一个“Team”,已知从每天诵读时间小于20分钟和大于或等于80分钟的所有学生中用分层抽样的方法抽取了5人,现从这5人中随机选取2人,求选取的两人能组成一个“Team”的概率.

参考答案:
【答案】(1) ![]() ;64(分钟).
;64(分钟).
(2) ![]() .
.
【解析】分析:(1)利用所有小矩形的面积之和为1,求出![]() 的值;(2)利用列举法求出选出的两人组成一个“team”的概率。
的值;(2)利用列举法求出选出的两人组成一个“team”的概率。
详解: (Ⅰ)∵各组数据的频率之和为1,即所有小矩形面积和为1,
∵![]() .解得
.解得![]()
∴诵读诗词的时间的平均数为
![]() (分钟)
(分钟)
(Ⅱ)由频率分布直方图,知![]() ,
,![]() ,
,![]() 内学生人数的频率之比为
内学生人数的频率之比为![]()
故5人中![]() ,
,![]() ,
,![]() 内学生人数分别为1,3,1.
内学生人数分别为1,3,1.
设![]() ,
,![]() ,
,![]() 内的5人依次为
内的5人依次为![]() 则抽取2人的所有基本事件有
则抽取2人的所有基本事件有
![]() 共10种情况.
共10种情况.
符合两同学能组成一个“ Team”的情况有![]() 共4种,
共4种,
故选取的两人能组成一个“Team”的概率为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】按照我国《机动车交通事故责任强制保险条例》规定,交强险是车主必须为机动车购买的险种,若普通7座以下私家车投保交强险第一年的费用(基准保费)统一为
 元,在下一年续保时,实行的是保费浮动机制,保费与上一、二、三个年度车辆发生道路交通事故的情况相关联,发生交通事故的次数越多,费率也就越高,具体浮动情況如表:
元,在下一年续保时,实行的是保费浮动机制,保费与上一、二、三个年度车辆发生道路交通事故的情况相关联,发生交通事故的次数越多,费率也就越高,具体浮动情況如表:
某机构为了研究某一品牌普通7座以下私家车的投保情况,随机抽取了80辆车龄已满三年的该品牌同型号私家车在下一年续保时的情况,统计得到了下面的表格:

以这80辆该品牌车的投保类型的频率代替一辆车投保类型的概率,完成下列问题:
(1)某家庭有一辆该品牌车且车龄刚满三年,记
 为该车在第四年续保时的费用,求
为该车在第四年续保时的费用,求 的分布列;
的分布列;(2)某销售商专门销售这一品牌的二手车,且将下一年的交强险保费高于基准保费的车辆记为事故车.
①若该销售商购进三辆车(车龄已满三年)该品牌二手车,求这三辆车中至少有2辆事故车的概率;
②假设购进一辆事故车亏损4000元,一辆非事故车盈利8000元.若该销售商一次购进100辆(车龄已满三年)该品牌二手车,求其获得利润的期望值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了解甲、乙两种离子在小鼠体内的残留程度,进行如下试验:将200只小鼠随机分成
 两组,每组100只,其中
两组,每组100只,其中 组小鼠给服甲离子溶液,
组小鼠给服甲离子溶液, 组小鼠给服乙离子溶液.每只小鼠给服的溶液体积相同、摩尔浓度相同.经过一段时间后用某种科学方法测算出残留在小鼠体内离子的百分比.根据试验数据分别得到如下直方图:
组小鼠给服乙离子溶液.每只小鼠给服的溶液体积相同、摩尔浓度相同.经过一段时间后用某种科学方法测算出残留在小鼠体内离子的百分比.根据试验数据分别得到如下直方图:
记
 为事件:“乙离子残留在体内的百分比不低于
为事件:“乙离子残留在体内的百分比不低于 ”,根据直方图得到
”,根据直方图得到 的估计值为
的估计值为 .
.(1)求乙离子残留百分比直方图中
 的值;
的值;(2)分别估计甲、乙离子残留百分比的平均值(同一组中的数据用该组区间的中点值为代表).
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系
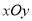 中,曲线
中,曲线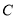 的参数方程为
的参数方程为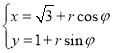 (
(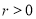 ,
,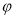 为参数),以坐标原点
为参数),以坐标原点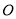 为极点,
为极点,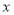 轴正半轴为极轴建立极坐标系,直线
轴正半轴为极轴建立极坐标系,直线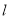 的极坐标方程为
的极坐标方程为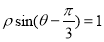 ,若直线
,若直线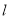 与曲线
与曲线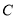 相切;
相切; (1)求曲线
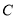 的极坐标方程与直线
的极坐标方程与直线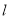 的直角坐标方程;
的直角坐标方程;(2)在曲线
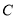 上取两点
上取两点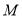 ,
,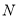 与原点
与原点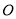 构成
构成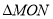 ,且满足
,且满足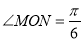 ,求
,求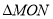 面积的最大值.
面积的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
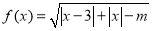 的定义域为
的定义域为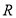 ;
;(1)求实数
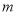 的取值范围;
的取值范围;(2)设实数
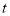 为
为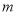 的最大值,若实数
的最大值,若实数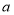 ,
,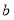 ,
,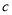 满足
满足 ,求
,求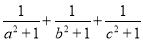 的最小值.
的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】给出下列四个命题:
①回归直线
 过样本点中心(
过样本点中心( ,
, )
)②将一组数据中的每个数据都加上或减去同一个常数后,平均值不变
③将一组数据中的每个数据都加上或减去同一个常数后,方差不变
④在回归方程
 =4x+4中,变量x每增加一个单位时,y平均增加4个单位
=4x+4中,变量x每增加一个单位时,y平均增加4个单位其中错误命题的序号是( )
A.①B.②C.③D.④
-
科目: 来源: 题型:
查看答案和解析>>【题目】某公司计划购买1台机器,该种机器使用三年后即被淘汰.机器有一易损零件,在购进机器时,可以额外购买这种零件作为备件,每个200元.在机器使用期间,如果备件不足再购买,则每个500元.现需决策在购买机器时应同时购买几个易损零件,为此搜集并整理了100台这种机器在三年使用期内更换的易损零件数,得下面柱状图:

记x表示1台机器在三年使用期内需更换的易损零件数,y表示1台机器在购买易损零件上所需的费用(单位:元),
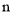 表示购机的同时购买的易损零件数.
表示购机的同时购买的易损零件数.(Ⅰ)若
 =19,求y与x的函数解析式;
=19,求y与x的函数解析式;(Ⅱ)若要求“需更换的易损零件数不大于
 ”的频率不小于0.5,求
”的频率不小于0.5,求 的最小值;
的最小值;(Ⅲ)假设这100台机器在购机的同时每台都购买19个易损零件,或每台都购买20个易损零件,分别计算这100台机器在购买易损零件上所需费用的平均数,以此作为决策依据,购买1台机器的同时应购买19个还是20个易损零件?
相关试题

