【题目】《中华人民共和国道路交通安全法》第47条的相关规定:机动车行经人行横道时,应当减速慢行;遇行人正在通过人行横道,应当停车让行,俗称“礼让斑马线”,《中华人民共和国道路交通安全法》 第90条规定:对不礼让行人的驾驶员处以扣3分,罚款50元的处罚.下表是某市一主干路口监控设备所抓拍的5个月内驾驶员不“礼让斑马线”行为统计数据:
月份 | 1 | 2 | 3 | 4 | 5 |
违章驾驶员人数 | 120 | 105 | 100 | 90 | 85 |
(1)请利用所给数据求违章人数y与月份之间的回归直线方程![]() +
+![]()
(2)预测该路口7月份的不“礼让斑马线”违章驾驶员人数;
(3)交警从这5个月内通过该路口的驾驶员中随机抽查了50人,调查驾驶员不“礼让斑马线”行为与驾龄的关系,得到如下2![]() 列联表:
列联表:
不礼让斑马线 | 礼让斑马线 | 合计 | |
驾龄不超过1年 | 22 | 8 | 30 |
驾龄1年以上 | 8 | 12 | 20 |
合计 | 30 | 20 | 50 |
能否据此判断有97.5![]() 的把握认为“礼让斑马线”行为与驾龄有关?
的把握认为“礼让斑马线”行为与驾龄有关?
参考公式及数据: ,
,![]() .
.
| 0.150 | 0.100 | 0.050 | 0.025 | 0.010 | 0.005 | 0.001 |
k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
![]() (其中n=a+b+c+d)
(其中n=a+b+c+d)
参考答案:
【答案】(1)![]() ;(2)66人;(3)有
;(2)66人;(3)有![]() 的把握认为“礼让斑马线”行为与驾龄关.
的把握认为“礼让斑马线”行为与驾龄关.
【解析】
(1)利用所给数据计算![]() 、
、![]() ,求出回归系数,写出回归直线方程;
,求出回归系数,写出回归直线方程;
(2)由(1)中的回归直线方程计算x=7时![]() 的值即可;
的值即可;
(3)由列联表中数据计算K2,对照临界值得出结论.
(1)由表中数据知,![]() ,
,
∴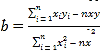
![]() ,
,
∴![]() ,
,
∴所求回归直线方程为![]() 。
。
(2)由(1)知,令![]() ,则
,则![]() 人.
人.
(3)由表中数据得![]()
![]() ,
,
根据统计有![]() 的把握认为“礼让斑马线”行为与驾龄关.
的把握认为“礼让斑马线”行为与驾龄关.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为调查某社区年轻人的周末生活状况,研究这一社区年轻人在周末的休闲方式与性别的关系,随机调查了该社区年轻人80人,得到下面的数据表:

(1)将此样本的频率估计为总体的概率,随机调查3名在该社区的年轻男性,设调查的3人在这一时间段以上网为休闲方式的人数为随机变量X,求X的分布列和数学期望;
(2)根据以上数据,能否有99%的把握认为“周末年轻人的休闲方式与性别有关系”?
参考公式:

参考数据:

0.05
0.010

3.841
6.635
-
科目: 来源: 题型:
查看答案和解析>>【题目】知函数
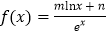 (
(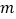 、
、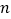 为常数),曲线
为常数),曲线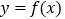 在点
在点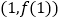 处的切线方程是
处的切线方程是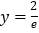 .
.(1)求
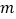 、
、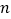 的值
的值 (2)求
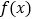 的最大值
的最大值(3)设
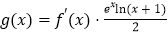 ,证明:对任意
,证明:对任意 ,都有
,都有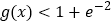 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】若由方程x2-y2=0和x2+(y-b)2=2所组成的方程组至多有两组不同的实数解,则实数b的取值范围是( )
A. b≥2
 或b≤-2
或b≤-2 B. b≥2或b≤-2
B. b≥2或b≤-2C. -2≤b≤2 D. -2
 ≤b≤2
≤b≤2
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆 C:
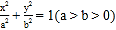 的焦距为2,且过点
的焦距为2,且过点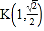 ,右焦点为
,右焦点为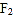 .设A,B 是C上的两个动点,线段 AB 的中点M 的横坐标为
.设A,B 是C上的两个动点,线段 AB 的中点M 的横坐标为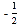 ,线段AB的中垂线交椭圆C于P,Q 两点.
,线段AB的中垂线交椭圆C于P,Q 两点.
(1)求椭圆 C 的方程;
(2)设M点纵坐标为m,求直线PQ的方程,并求
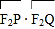 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系
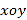 中,点
中,点 ,直线
,直线 ,设圆
,设圆 的半径为1, 圆心在
的半径为1, 圆心在 上.
上.
(1)若圆心
 也在直线
也在直线 上,过点
上,过点 作圆
作圆 的切线,求切线方程;
的切线,求切线方程;(2)若圆
 上存在点
上存在点 ,使
,使 ,求圆心
,求圆心 的横坐标
的横坐标 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】在直角坐标系xOy 中,曲线C1的参数方程为:
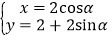 (
( ),M是
),M是 上的动点,P点满足
上的动点,P点满足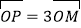 ,P点的轨迹为曲线.
,P点的轨迹为曲线.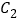
(1)求
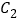 的参数方程;
的参数方程;(2)在以O为极点,x 轴的正半轴为极轴的极坐标系中,射线
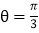 与
与 的异于极点的交点为A,与
的异于极点的交点为A,与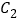 的异于极点的交点为B,求
的异于极点的交点为B,求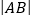 .
.
相关试题

