【题目】某校高三(1)班在一次语文测试结束后,发现同学们在背诵内容方面失分较为严重.为了提升背诵效果,班主任倡议大家在早、晚读时间站起来大声诵读,为了解同学们对站起来大声诵读的态度,对全班50名同学进行调查,将调查结果进行整理后制成下表:
考试分数 |
|
|
|
|
|
|
频数 | 5 | 10 | 15 | 5 | 10 | 5 |
赞成人数 | 4 | 6 | 9 | 3 | 6 | 4 |
(1)欲使测试优秀率为30%,则优秀分数线应定为多少分?
(2)依据第1问的结果及样本数据研究是否赞成站起来大声诵读的态度与考试成绩是否优秀的关系,列出2×2列联表,并判断是否有90%的把握认为赞成与否的态度与成绩是否优秀有关系.
参考公式及数据: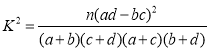 ,
,![]() .
.
| 0.100 | 0.050 | 0.025 | 0.010 |
| 2.706 | 3.841 | 5.024 | 6.635 |
参考答案:
【答案】(1)125分(2)列联表见解析;没有90%的把握认为赞成与否的态度与成绩是否优秀有关系
【解析】
(1)根据题意,测试的优秀率为30%,所以测试成绩优秀的人数为![]() ,即可得答案;
,即可得答案;
(2)完成列联表,再代入卡方系数计算公式,即可得答案.
(1)因为测试的优秀率为30%,所以测试成绩优秀的人数为![]() ,
,
所以优秀分数线应定为125分.
(2)由(1)知,测试成绩优秀的学生有![]() 人,其中“赞成的”有10人;测试成绩不优秀的学生有
人,其中“赞成的”有10人;测试成绩不优秀的学生有![]() 人,其中“赞成的”有22人.
人,其中“赞成的”有22人.
2×2列联表如下:
赞成 | 不赞成 | 合计 | |
优秀 | 10 | 5 | 15 |
不优秀 | 22 | 13 | 35 |
合计 | 32 | 18 | 50 |
![]()
因此,没有90%的把握认为赞成与否的态度与成绩是否优秀有关系.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 .
.(1)讨论
 的单调性;
的单调性;(2)若
 ,直线
,直线 与曲线
与曲线 和曲线
和曲线 都相切,切点分别为
都相切,切点分别为 ,
, ,求证:
,求证: .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】“中国剩余定理”又称“孙子定理”,最早可见于中国南北朝时期的数学著作《孙子算经》卷下第二十六题,叫做“物不知数”,原文如下:今有物不知其数,三三数之剩二,五五数之剩三,七七数之剩二.问物几何?现有这样一个相关的问题:将1到2020这2020个自然数中被5除余3且被7除余2的数按照从小到大的顺序排成一列,构成一个数列,则该数列各项之和为( )
A.56383B.57171C.59189D.61242
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在三棱锥A﹣BCD中,点E在BD上,EA=EB=EC=ED,BD
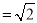 CD,△ACD为正三角形,点M,N分别在AE,CD上运动(不含端点),且AM=CN,则当四面体C﹣EMN的体积取得最大值
CD,△ACD为正三角形,点M,N分别在AE,CD上运动(不含端点),且AM=CN,则当四面体C﹣EMN的体积取得最大值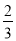 时,三棱锥A﹣BCD的外接球的表面积为_____.
时,三棱锥A﹣BCD的外接球的表面积为_____.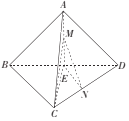
-
科目: 来源: 题型:
查看答案和解析>>【题目】设抛物线
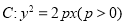 的焦点为
的焦点为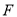 ,准线为
,准线为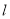 ,
,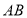 为过焦点
为过焦点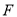 且垂直于
且垂直于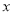 轴的抛物线
轴的抛物线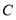 的弦,已知以
的弦,已知以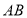 为直径的圆经过点
为直径的圆经过点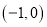 .
.(1)求
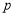 的值及该圆的方程;
的值及该圆的方程;(2)设
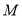 为
为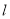 上任意一点,过点
上任意一点,过点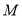 作
作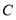 的切线,切点为
的切线,切点为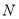 ,证明:
,证明: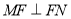 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】对某两名高三学生在连续9次数学测试中的成绩(单位:分)进行统计得到折线图,下面是关于这两位同学的数学成绩分析.
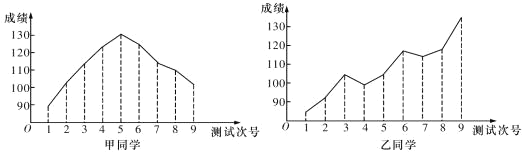
①甲同学的成绩折线图具有较好的对称性,故平均成绩为130分;
②根据甲同学成绩折线图提供的数据进行统计,估计该同学平均成绩在区间
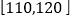 内;
内;③乙同学的数学成绩与测试次号具有比较明显的线性相关性,且为正相关;
④乙同学连续九次测验成绩每一次均有明显进步.
其中正确的个数为( )
A.
 B.
B. C.
C.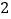 D.
D.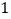
-
科目: 来源: 题型:
查看答案和解析>>【题目】在
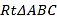 中,
中,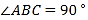 ,
,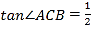 .已知
.已知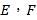 分别是
分别是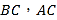 的中点.将
的中点.将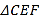 沿
沿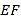 折起,使
折起,使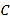 到
到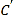 的位置且二面角
的位置且二面角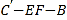 的大小是60°,连接
的大小是60°,连接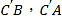 ,如图:
,如图: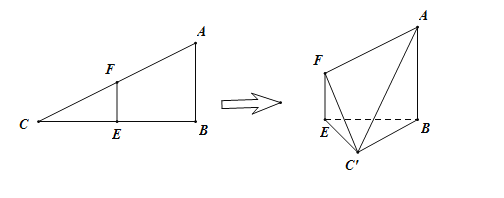
(1)证明:平面
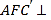 平面
平面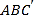
(2)求平面
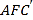 与平面
与平面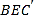 所成二面角的大小.
所成二面角的大小.
相关试题

