【题目】如图,在以![]() 为顶点的五面体中,O为AB的中点,
为顶点的五面体中,O为AB的中点,
![]() 平面
平面![]() ,
, ![]() ∥
∥![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
(1)在图中过点O作平面![]() ,使得
,使得![]() ∥平面
∥平面![]() ,并说明理由;
,并说明理由;
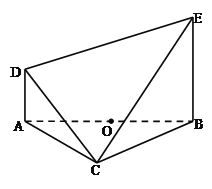
(2)求直线DE与平面CBE所成角的正切值.
参考答案:
【答案】(1)见解析;(2)![]()
【解析】试题分析:(1)在BE上取点F,使得![]() ,在BC上取点H,使
,在BC上取点H,使![]() ,平面OFH即为所求的平面
,平面OFH即为所求的平面![]() 取BE的中点G,连接AG,再证明
取BE的中点G,连接AG,再证明![]() ∥平面
∥平面![]() 即可;(2)先证明
即可;(2)先证明![]() 是
是![]() 与平面
与平面![]() 所成的角,根据
所成的角,根据![]() 与平面
与平面![]() 所成的角等于
所成的角等于![]() 与平面
与平面![]() 所成的角,利用直角三角形性质可得结果.
所成的角,利用直角三角形性质可得结果.
试题解析:(1)如图,在BE上取点F,使得![]() ,在BC上取点H,使
,在BC上取点H,使![]() ,连接OF,FH,OH,则平面OFH即为所求的平面
,连接OF,FH,OH,则平面OFH即为所求的平面![]() .
.
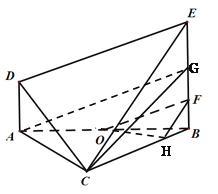
理由如下:
取BE的中点G,连接AG,
![]() ,
, ![]() 为
为![]() 中点,
中点, ![]()
![]() ∥
∥![]()
![]() ∥
∥![]() ,
, ![]() 是平行四边形,
是平行四边形,
![]()
![]() ∥
∥![]()
![]() 中,
中, ![]() 是
是![]() 中点,
中点, ![]() 是
是![]() 中点,
中点,
所以![]() 是中位线,
是中位线,![]() ∥
∥![]()
![]() ∥
∥![]() ,
,
![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,
,
![]() ∥平面
∥平面![]() .
.
又![]() 中,
中, ![]() ,
, ![]() ,
,
![]() ,
, ![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,
,
![]() 平面
平面![]() ,
,
又![]() ,
, ![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,
,
![]() 平面
平面![]() 平面
平面![]() ,即
,即![]() ∥平面
∥平面![]() .
.
(2)连接![]() ,因为
,因为![]() 平面
平面![]() ,
,
又![]() ∥
∥![]() ,所以
,所以![]() 平面
平面![]() ,
, ![]()
又![]()
![]() 平面
平面![]()
![]() 是
是![]() 与平面
与平面![]() 所成的角,
所成的角,
![]() ∥
∥![]() ,
,
![]()
![]() 与平面
与平面![]() 所成的角等于
所成的角等于![]() 与平面
与平面![]() 所成的角
所成的角
在![]() 中,
中, ![]() ,
, ![]() ,
, ![]()
![]() 在
在![]() 中,
中, ![]()
![]() 在
在![]() 中,
中, ![]()
即直线DE与平面CBE所成角的正切值为![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】在四边形
 中,已知
中,已知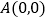 ,
,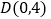 ,点
,点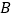 在
在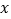 轴上,
轴上,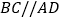 ,且对角线
,且对角线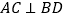 .
.(1)求点
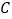 的轨迹
的轨迹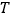 的方程;
的方程;(2)若点
 是直线
是直线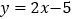 上任意一点,过点
上任意一点,过点 作点
作点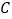 的轨迹
的轨迹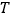 的两切线
的两切线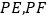 ,
,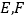 为切点,直线
为切点,直线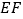 是否恒过一定点?若是,请求出这个定点的坐标;若不是,请说明理由.
是否恒过一定点?若是,请求出这个定点的坐标;若不是,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】根据国家环保部新修订的《环境空气质量标准》规定:居民区
 的年平均浓度不得超过
的年平均浓度不得超过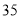 微克/立方米,
微克/立方米,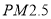 的24小时平均浓度不得超过
的24小时平均浓度不得超过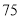 微克/立方米.某城市环保部门随机抽取了一居民区去年20天
微克/立方米.某城市环保部门随机抽取了一居民区去年20天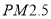 的24小时平均浓度的监测数据,数据统计如下:
的24小时平均浓度的监测数据,数据统计如下:组别
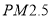 浓度
浓度(微克/立方米)
频数(天)
频率
第一组
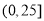
3
0.15
第二组

12
0.6
第三组

3
0.15
第四组
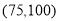
2
0.1
(1)从样本中
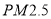 的24小时平均浓度超过50微克/立方米的5天中,随机抽取2天,求恰好有一天
的24小时平均浓度超过50微克/立方米的5天中,随机抽取2天,求恰好有一天 的24小时平均浓度超过75微克/立方米的概率;
的24小时平均浓度超过75微克/立方米的概率;(2)求样本平均数,并根据样本估计总体的思想,从
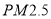 的年平均浓度考虑,判断该居民区的环境是
的年平均浓度考虑,判断该居民区的环境是否需要改进?说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知A(4, 0),B(2, 2),C (6, 0),记△ABC的外接圆为⊙P.
(1)求⊙P的方程.
(2)对于线段PA上的任意一点G,是否存在以B为圆心的圆,在圆B上总能找到不同的两点E、F,满足
 =
=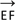 ,若存在,求圆B的半径
,若存在,求圆B的半径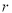 的取值范围;若不存在,说明理由.
的取值范围;若不存在,说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
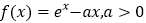 .
.(1)记
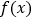 的极小值为
的极小值为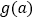 ,求
,求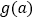 的最大值;
的最大值;(2)若对任意实数
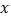 恒有
恒有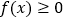 ,求
,求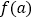 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知直角梯形ABCD中,AD∥BC,∠ADC=90°,A(-3,-10),
B (-2,-1),C(3,4),
(1)求边AD和CD所在的直线方程;
(2)数列
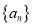 的前
的前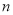 项和为
项和为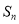 ,点
,点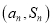 在直线CD上,求证
在直线CD上,求证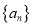 为等比数列.
为等比数列. -
科目: 来源: 题型:
查看答案和解析>>【题目】某校高一(1)班有男同学45名,女同学15名,老师按照分层抽样的方法抽取4人组建了一个课外兴趣小组.
(I)求课外兴趣小组中男、女同学的人数;
(II)经过一个月的学习、讨论,这个兴趣小组决定选出两名同学做某项实验,方法是从小组里选出一名同学做实验,该同学做完后,再从小组内剩下的同学中选出一名同学做实验,求选出的两名同学中恰有一名女同学的概率;
(III)在(II)的条件下,第一次做实验的同学A得到的实验数据为38,40,41,42,44,第二次做实验的同学B得到的实验数据为39,40,40,42,44,请问哪位同学的实验更稳定?并说明理由.
相关试题

