【题目】已知方程![]() 的四个根组成一个首项为
的四个根组成一个首项为![]() 的等差数列,则
的等差数列,则![]() _____.
_____.
参考答案:
【答案】![]()
【解析】
把方程(x2﹣2x+m)(x2﹣2x+n)=0化为x2﹣2x+m=0,或x2﹣2x+n=0,设![]() 是第一个方程
是第一个方程
的根,代入方程即可求得m,则方程的另一个根可求;设另一个方程的根为s,t,(s≤t)
根据韦达定理可知∴s+t=2![]() 根据等差中项的性质可知四个跟成的等差数列为
根据等差中项的性质可知四个跟成的等差数列为![]() ,s,t,
,s,t,
![]() ,进而根据数列的第一项和第四项求得公差,则s和t可求,进而根据韦达定理求得n,最
,进而根据数列的第一项和第四项求得公差,则s和t可求,进而根据韦达定理求得n,最
后代入|m﹣n|即可.
方程(x2﹣2x+m)(x2﹣2x+n)=0可化为
x2﹣2x+m=0①,或x2﹣2x+n=0②,
设![]() 是方程①的根,
是方程①的根,
则将![]() 代入方程①,可解得m
代入方程①,可解得m![]() ,
,
∴方程①的另一个根为![]() .
.
设方程②的另一个根为s,t,(s≤t)
则由根与系数的关系知,s+t=2,st=n,
又方程①的两根之和也是2,
∴s+t![]()
由等差数列中的项的性质可知,
此等差数列为![]() ,s,t,
,s,t,![]() ,
,
公差为[![]() ]÷3
]÷3![]() ,
,
∴s![]() ,t
,t![]() ,
,
∴n=st![]()
∴,|m﹣n|=|![]() |
|![]() .
.
故答案为:![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在底面为矩形的四棱锥
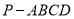 中,
中,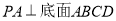 ,
,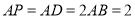 ,且
,且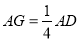 ,其中
,其中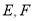 分别是线段
分别是线段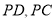 的中点。
的中点。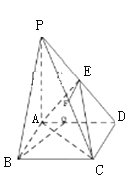
(1)证明:
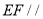 平面
平面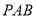
(2)证明:
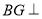 平面
平面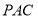
(3)求:直线
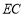 与平面
与平面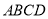 所成角的正弦值
所成角的正弦值 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是圆O的直径,点C是圆O上异于A,B的点,直线PC⊥平面ABC,E,F分别是PA,PC的中点.
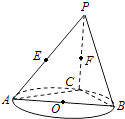
(1)记平面BEF与平面ABC的交线为l,试判断直线l与平面PAC的位置关系,并加以证明;
(2)设(1)中的直线l与圆O的另一个交点为D,且点Q满足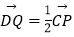 .记直线PQ与平面ABC所成的角为θ,异面直线PQ与EF所成的角为α,二面角E﹣l﹣C的大小为β.求证:sinθ=sinαsinβ.
.记直线PQ与平面ABC所成的角为θ,异面直线PQ与EF所成的角为α,二面角E﹣l﹣C的大小为β.求证:sinθ=sinαsinβ. -
科目: 来源: 题型:
查看答案和解析>>【题目】假设每天从甲地去乙地的旅客人数X是服从正态分布N(800,502)的随机变量.记一天中从甲地去乙地的旅客人数不超过900的概率为p0 .
(1)求p0的值;
(参考数据:若X~N(μ,σ2),有P(μ﹣σ<X≤μ+σ)=0.6826,P(μ﹣2σ<X≤μ+2σ)=0.9544,P(μ﹣3σ<X≤μ+3σ)=0.9974.)
(2)某客运公司用A,B两种型号的车辆承担甲、乙两地间的长途客运业务,每车每天往返一次,A,B两种车辆的载客量分别为36人和60人,从甲地去乙地的营运成本分别为1600元/辆和2400元/辆.公司拟组建一个不超过21辆车的客运车队,并要求B型车不多于A型车7辆.若每天要以不小于p0的概率运完从甲地去乙地的旅客,且使公司从甲地去乙地的营运成本最小,那么应配备A型车、B型车各多少辆? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知椭圆C1与C2的中心在坐标原点O,长轴均为MN且在x轴上,短轴长分别为2m,2n(m>n),过原点且不与x轴重合的直线l与C1 , C2的四个交点按纵坐标从大到小依次为A,B,C,D,记
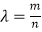 ,△BDM和△ABN的面积分别为S1和S2 .
,△BDM和△ABN的面积分别为S1和S2 . 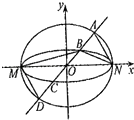
(1)当直线l与y轴重合时,若S1=λS2 , 求λ的值;
(2)当λ变化时,是否存在与坐标轴不重合的直线l,使得S1=λS2?并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】设数列{an}满足a1=2,an+1-an=3·22n-1.
(1)求数列{an}的通项公式;
(2)令bn=nan,求数列{bn}的前n项和Sn.
-
科目: 来源: 题型:
查看答案和解析>>【题目】现有10道题,其中6道甲类题,4道乙类题,张同学从中任取3道题解答.
(I)求张同学至少取到1道乙类题的概率;
(II)已知所取的3道题中有2道甲类题,1道乙类题.设张同学答对甲类题的概率都是
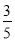 ,答对每道乙类题的概率都是
,答对每道乙类题的概率都是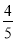 ,且各题答对与否相互独立.用
,且各题答对与否相互独立.用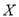 表示张同学答对题的个数,求
表示张同学答对题的个数,求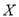 的分布列和数学期望.
的分布列和数学期望.
相关试题

