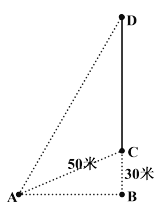
【题目】某城市的电视发射搭CD建在市郊的一座小山上,如图所示,小山高BC为30米,在地平面上有一点A,测得A,C两点间距离为50米.

(1)如果从点A观测电视发射塔的视角∠CAD=![]() ,求这座电视发射塔的高度;
,求这座电视发射塔的高度;
(2)点A在何位置时,角∠CAD最大.(参考数据:![]() )
)
参考答案:
【答案】(1)![]() ;(2)点
;(2)点![]() 距离
距离![]() 点为
点为![]()
【解析】
(1)首先由已知可得![]() ,设
,设![]() ,再根据锐角三角函数与两角和的正切公式计算可得;
,再根据锐角三角函数与两角和的正切公式计算可得;
(2)设点![]() 、
、![]() 的距离为
的距离为![]() ,
,![]() ,再根据两角差的正切公式及锐角三角函数的定义得到
,再根据两角差的正切公式及锐角三角函数的定义得到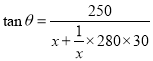 ,令
,令![]() ,利用基本不等式求出
,利用基本不等式求出![]() 的最小值,即可得到
的最小值,即可得到![]() 的最大值;
的最大值;
解:(1)![]() ,
,![]() ,
,![]() ,所以
,所以![]() ,设
,设![]()
![]() ,
,![]()
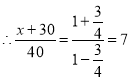 ,
,![]() ,
,![]() 塔高
塔高![]()
(2)设点![]() 、
、![]() 的距离为
的距离为![]() ,
,![]() ,
,
则![]()
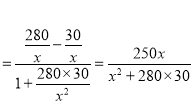 ,即
,即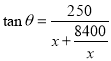 ,
,
令![]() ,因为
,因为![]() ,所以
,所以![]()
所以当且仅当![]() 时,即
时,即![]() 时,
时, ![]() 取得最大,
取得最大,
![]() 是单调递增函数,
是单调递增函数,
所以点![]() 距离
距离![]() 点为
点为![]() 时,
时,![]() 取得最大值;
取得最大值;
-
科目: 来源: 题型:
查看答案和解析>>【题目】设椭圆
 的离心率为
的离心率为 ,左顶点到直线
,左顶点到直线 的距离为
的距离为 .
.(Ⅰ)求椭圆C的方程;
(Ⅱ)设直线
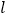 与椭圆C相交于A、B两点,若以AB为直径的圆经过坐标原点O,试探究:点O到直线AB的距离是否为定值?若是,求出这个定值;否则,请说明理由;
与椭圆C相交于A、B两点,若以AB为直径的圆经过坐标原点O,试探究:点O到直线AB的距离是否为定值?若是,求出这个定值;否则,请说明理由;(Ⅲ)在(Ⅱ)的条件下,试求△AOB面积S的最小值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设F为抛物线
 的焦点,A,B,C为该抛物线上三点,若
的焦点,A,B,C为该抛物线上三点,若 ,则
,则 = ( )
= ( )A. 9 B. 6 C. 4 D. 3
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线
 ,直线
,直线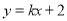 与E交于A、B两点,且
与E交于A、B两点,且 ,其中O为原点.
,其中O为原点.(1)求抛物线E的方程;
(2)点C坐标为
 ,记直线CA、CB的斜率分别为
,记直线CA、CB的斜率分别为 ,证明:
,证明:  为定值.
为定值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图是一个几何体的平面展开图,其中四边形ABCD为正方形,△PDC, △PBC, △PAB, △PDA为全等的等边三角形,E、F分别为PA、PD的中点,在此几何体中,下列结论中错误的为 ( )

A. 平面BCD⊥平面PAD B. 直线BE与直线AF是异面直线
C. 直线BE与直线CF共面 D. 面PAD与面PBC的交线与BC平行
-
科目: 来源: 题型:
查看答案和解析>>【题目】关于函数
 有如下命题:
有如下命题:①
 ; ②函数的图象关于原点中心对称;
; ②函数的图象关于原点中心对称;③函数的定义域与值域相同; ④函数的图象必经过第二、四象限.
其中正确命题的个数是( )
A.4B.3C.2D.1
-
科目: 来源: 题型:
查看答案和解析>>【题目】若对于曲线
 上任意点处的切线
上任意点处的切线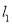 ,总存在
,总存在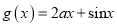 上处的切线
上处的切线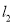 ,使得
,使得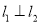 ,则实数
,则实数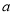 的取值范围是__________.
的取值范围是__________.
相关试题

