【题目】设点![]() ,直线
,直线![]() ,点
,点![]() 在直线
在直线![]() 上移动,
上移动, ![]() 是线段
是线段![]() 与
与![]() 轴的交点,
轴的交点, ![]() .
.
(Ⅰ) 求动点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(Ⅱ)直线![]() 与
与![]() 轴相交于点
轴相交于点![]() ,过
,过![]() 的直线
的直线![]() 交轨迹
交轨迹![]() 于
于![]() 两点,
两点,
试探究点![]() 与以
与以![]() 为直径的圆的位置关系,并加以说明.
为直径的圆的位置关系,并加以说明.
参考答案:
【答案】(1)![]() (2)点
(2)点![]() 在以
在以![]() 为直径的圆上或外
为直径的圆上或外
【解析】试题分析:(1)由垂直平分线性质将条件转化为![]() .再根据抛物线定义可得动点
.再根据抛物线定义可得动点![]() 的轨迹
的轨迹![]() 是以
是以![]() 为焦点,
为焦点, ![]() 为准线的抛物线,最后根据性质求抛物线标准方程(2)直径AB中点即圆心到直线
为准线的抛物线,最后根据性质求抛物线标准方程(2)直径AB中点即圆心到直线![]() 的距离等于A、B两点到直线
的距离等于A、B两点到直线![]() 的距离和的一半,而由抛物线定义有A、B两点到直线
的距离和的一半,而由抛物线定义有A、B两点到直线![]() 的距离和为
的距离和为![]() ,因此以
,因此以![]() 为直径的圆与直线
为直径的圆与直线![]() 相切,进而可判断点
相切,进而可判断点![]() 与以
与以![]() 为直径的圆的位置关系
为直径的圆的位置关系
试题解析:解:(Ⅰ)依题意知: ![]() 是线段
是线段![]() 的垂直平分线.∴
的垂直平分线.∴![]() 是点
是点![]() 到直线
到直线![]() 的距离.∵点
的距离.∵点![]() 在线段
在线段![]() 的垂直平分线,∴
的垂直平分线,∴![]() .
.
故动点![]() 的轨迹
的轨迹![]() 是以
是以![]() 为焦点,
为焦点, ![]() 为准线的抛物线, 其方程为:
为准线的抛物线, 其方程为: ![]() .
.
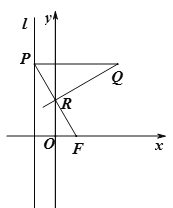
(Ⅱ)法一:设A、B两点到直线![]() 的距离分别为
的距离分别为![]() ,
,
直径AB中点N到直线![]() 的距离分别为
的距离分别为![]() ,
,
由抛物线定义知![]() , ∴
, ∴![]()
∴以![]() 为直径的圆与直线
为直径的圆与直线![]() 相切
相切
法二:

(1)当AB垂直![]() 轴时,以
轴时,以![]() 为直径的圆
为直径的圆![]() 点
点![]() 为切点,
为切点,
∴点![]() 与以
与以![]() 为直径的圆上
为直径的圆上
(2)当直线![]() 与
与![]() 轴不垂直时,
轴不垂直时, ![]() ∴点
∴点![]() 与以
与以![]() 为直径的圆外
为直径的圆外
①当直线AB垂直于![]() 轴时,易知以
轴时,易知以![]() 为直径的圆方程为
为直径的圆方程为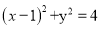 ,
,
点![]() 满足方程,∴点
满足方程,∴点![]() 与以
与以![]() 为直径的圆上
为直径的圆上
②当直线![]() 与
与![]() 轴不垂直时,
轴不垂直时,
设直线AB方程为![]() 与抛物线交点
与抛物线交点![]() ,
, ![]() ,
,
联立![]()
![]() ,
,
显然![]() 且
且![]() , 圆直径
, 圆直径![]()
AB中点N的坐标(![]() ,
,
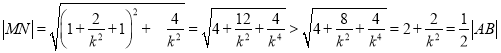 ,∴点
,∴点![]() 与以
与以![]() 为直径的圆外
为直径的圆外
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 是R上的奇函数,且
是R上的奇函数,且 的图象关于
的图象关于 对称,当
对称,当 时,
时,  ,
,(Ⅰ)当
 时,求
时,求 的解析式;
的解析式;(Ⅱ)计算
 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,P是双曲线
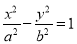 (a>0,b>0,xy≠0)上的动点,F1,F2是双曲线的焦点,M是∠F1PF2的平分线上一点,且
(a>0,b>0,xy≠0)上的动点,F1,F2是双曲线的焦点,M是∠F1PF2的平分线上一点,且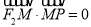 .某同学用以下方法研究|OM|:延长F2M交PF1于点N,可知△PNF2为等腰三角形,且M为F2N的中点,得|OM|=
.某同学用以下方法研究|OM|:延长F2M交PF1于点N,可知△PNF2为等腰三角形,且M为F2N的中点,得|OM|=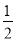 |NF1|=…=a。类似地:P是椭圆
|NF1|=…=a。类似地:P是椭圆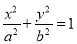 (a>b>0,xy≠0)上的动点,F1,F2是椭圆的焦点,M是∠F1PF2的平分线上一点,且
(a>b>0,xy≠0)上的动点,F1,F2是椭圆的焦点,M是∠F1PF2的平分线上一点,且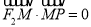 ,则|OM|的取值范围是________.
,则|OM|的取值范围是________.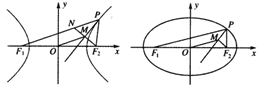
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
 经过点
经过点 ,且两焦点与短轴的一个端点构成等腰直角三角形.
,且两焦点与短轴的一个端点构成等腰直角三角形. (Ⅰ)求椭圆的方程;
(Ⅱ)若圆
 的任意一条切线
的任意一条切线 与椭圆E相交于P,Q两点,试问:
与椭圆E相交于P,Q两点,试问: 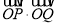 是否为定值? 若是,求这个定值;若不是,说明理由.
是否为定值? 若是,求这个定值;若不是,说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示的“8”字形曲线是由两个关于x轴对称的半圆和一个双曲线的一部分组成的图形,其中上半个圆所在圆方程是x2+y2﹣4y﹣4=0,双曲线的左、右顶
点A、B是该圆与x轴的交点,双曲线与半圆相交于与x轴平行的直径的两端点.
(1)试求双曲线的标准方程;
(2)记双曲线的左、右焦点为F1、F2 , 试在“8”字形曲线上求点P,使得
∠F1PF2是直角.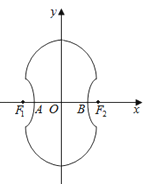
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=﹣alnx+
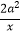 +x(a≠0)
+x(a≠0)
(I)若曲线y=f(x)在点(1,f(1)))处的切线与直线x﹣2y=0垂直,求实数a的值;
(Ⅱ)讨论函数f(x)的单调性;
(Ⅲ)当a∈(﹣∞,0)时,记函数f(x)的最小值为g(a),求证:g(a)≤﹣e﹣4 . -
科目: 来源: 题型:
查看答案和解析>>【题目】已知等差数列{an}的各项均为正数,且Sn=
 +
+  +…+
+…+  ,S2=
,S2=  ,S3=
,S3=  .设[x]表示不大于x的最大整数(如[2.10]=2,[0.9]=0).
.设[x]表示不大于x的最大整数(如[2.10]=2,[0.9]=0).
(1)试求数列{an}的通项;
(2)求T=[log21]+[log22]+[log23]+…+[log2( ﹣1)]+[log2(
﹣1)]+[log2(  )]关于n的表达式.
)]关于n的表达式.
相关试题

