【题目】已知函数f(x)=Asin(ωx+φ)(x∈R,ω>0,0<φ< ![]() )的部分图象如图所示.
)的部分图象如图所示. 
(1)求函数f(x)的解析式;
(2)求函数g(x)=f(x﹣ ![]() )﹣f(x+
)﹣f(x+ ![]() )的单调递增区间.
)的单调递增区间.
参考答案:
【答案】
(1)解:由图象可知,周期T=2( ![]() ﹣
﹣ ![]() )=π,∴ω=
)=π,∴ω= ![]() =2
=2
∵点( ![]() ,0)在函数图象上,∴Asin(2×
,0)在函数图象上,∴Asin(2× ![]() +φ)=0
+φ)=0
∴sin( ![]() +φ)=0,∴
+φ)=0,∴ ![]() +φ=π+kπ,即φ=kπ+
+φ=π+kπ,即φ=kπ+ ![]() ,k∈z
,k∈z
∵0<φ< ![]()
∴φ= ![]()
∵点(0,1)在函数图象上,∴Asin ![]() =1,A=2
=1,A=2
∴函数f(x)的解析式为f(x)=2sin(2x+ ![]() )
)
(2)解:g(x)=2sin[2(x﹣ ![]() )+
)+ ![]() ]﹣2sin[2(x+
]﹣2sin[2(x+ ![]() )+
)+ ![]() ]=2sin2x﹣2sin(2x+
]=2sin2x﹣2sin(2x+ ![]() )
)
=2sin2x﹣2( ![]() sin2x+
sin2x+ ![]() cos2x)=sin2x﹣
cos2x)=sin2x﹣ ![]() cos2x
cos2x
=2sin(2x﹣ ![]() )
)
由﹣ ![]() +2kπ≤2x﹣
+2kπ≤2x﹣ ![]() ≤
≤ ![]() +2kπ,k∈z
+2kπ,k∈z
得kπ﹣ ![]() ≤x≤kπ+
≤x≤kπ+ ![]()
∴函数g(x)=f(x﹣ ![]() )﹣f(x+
)﹣f(x+ ![]() )的单调递增区间为[kπ﹣
)的单调递增区间为[kπ﹣ ![]() ,kπ+
,kπ+ ![]() ]k∈z
]k∈z
【解析】(1)先利用函数图象求此函数的周期,从而计算得ω的值,再将点( ![]() ,0)和(0,1)代入解析式,分别解得φ和A的值,最后写出函数解析式即可;(2)先利用三角变换公式将函数g(x)的解析式化为y=Asin(ωx+φ)型函数,再将内层函数看做整体,置于外层函数即正弦函数的单调增区间上,即可解得函数g(x)的单调增区间
,0)和(0,1)代入解析式,分别解得φ和A的值,最后写出函数解析式即可;(2)先利用三角变换公式将函数g(x)的解析式化为y=Asin(ωx+φ)型函数,再将内层函数看做整体,置于外层函数即正弦函数的单调增区间上,即可解得函数g(x)的单调增区间
-
科目: 来源: 题型:
查看答案和解析>>【题目】(本小题满分10分)
已知如下等式:
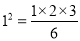 ,
, 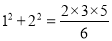 ,
, 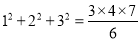 ,
,当
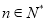 时,试猜想
时,试猜想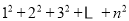 的值,并用数学归纳法给予证明.
的值,并用数学归纳法给予证明. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 .
.(I)讨论函数的单调性,并证明当
 时,
时, 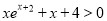 ;
;(Ⅱ)证明:当
 时,函数
时,函数 有最小值,设
有最小值,设 最小值为
最小值为 ,求函数
,求函数 的值域.
的值域. -
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两家商场对同一种商品开展促销活动,对购买该商品的顾客两家商场的奖励方案如下:
甲商场:顾客转动如图所示圆盘,当指针指向阴影部分(图中两个阴影部分均为扇形,且每个扇形圆心角均为
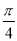 ,边界忽略不计)即为中奖·
,边界忽略不计)即为中奖·乙商场:从装有2个白球、2个蓝球和2个红球的盒子中一次性摸出1球(这些球除颜色外完全相同),它是红球的概率是
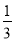 ,若从盒子中一次性摸出2球,且摸到的是2个相同颜色的球,即为中奖.
,若从盒子中一次性摸出2球,且摸到的是2个相同颜色的球,即为中奖.
(Ⅰ)求实数
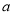 的值;
的值;(Ⅱ)试问:购买该商品的顾客在哪家商场中奖的可能性大?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某中学组织了一次高二文科学生数学学业水平模拟测试,学校从测试合格的男、女生中各随机抽取100人的成绩进行统计分析,分别制成了如图所示的男生和女生数学成绩的频率分布直方图.

(Ⅰ)若所得分数大于等于80分认定为优秀,求男、女生优秀人数各有多少人?
(Ⅱ)在(Ⅰ)中的优秀学生中用分层抽样的方法抽取5人,从这5人中任意任取2人,求至少有一名男生的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知数列
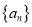 的前
的前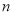 项和为
项和为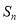 ,且
,且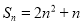 ,
, 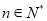 ,在数列
,在数列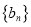 中,
中, 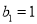 ,
, 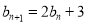 ,
, 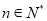 .
.(1)求证:
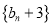 是等比数列;
是等比数列;(2)若
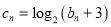 ,求数列
,求数列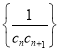 的前
的前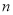 项和
项和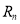 ;
;(3)求数列
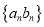 的前
的前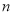 项和
项和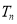 .
. -
科目: 来源: 题型:
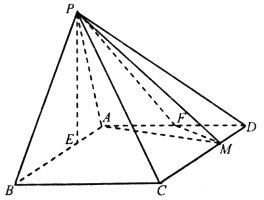
查看答案和解析>>【题目】在四棱锥
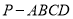 中,底面
中,底面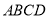 为平行四边形,
为平行四边形, 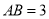 ,
, 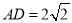 ,
, 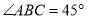 ,
, 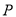 点在底面
点在底面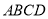 内的射影
内的射影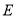 在线段
在线段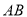 上,且
上,且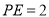 ,
, 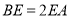 ,
, 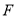 为
为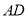 的中点,
的中点, 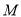 在线段
在线段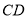 上,且
上,且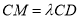 .
. 
(Ⅰ)当
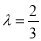 时,证明:平面
时,证明:平面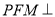 平面
平面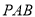 ;
;(Ⅱ)当平面
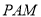 与平面
与平面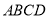 所成的二面角的正弦值为
所成的二面角的正弦值为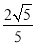 时,求四棱锥
时,求四棱锥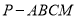 的体积.
的体积.
相关试题

