【题目】在平面直角坐标系![]() 中,点
中,点![]() ,直线
,直线![]() 与动直线
与动直线![]() 的交点为
的交点为![]() ,线段
,线段![]() 的中垂线与动直线
的中垂线与动直线![]() 的交点为
的交点为![]() .
.
(1)求动点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)过动点![]() 作曲线
作曲线![]() 的两条切线,切点分别为
的两条切线,切点分别为![]() ,
, ![]() ,求证:
,求证: ![]() 的大小为定值.
的大小为定值.

参考答案:
【答案】(1)曲线![]() 的方程为
的方程为![]() .(2)详见解析
.(2)详见解析
【解析】试题分析:根据题意动点到定点距离等于到定直线距离,符合抛物线定义,写出抛物线方程,第二步设出直线方程,联立方程组,根据根与系数关系可得![]() ,可知
,可知![]() 为定值.
为定值.
试题解析:(1)因为直线![]() 与
与![]() 垂直,所以
垂直,所以![]() 为点
为点![]() 到直线
到直线![]() 的距离.
的距离.
连结![]() ,因为
,因为![]() 为线段
为线段![]() 的中垂线与直线
的中垂线与直线![]() 的交点,所以
的交点,所以![]() .
.
所以点![]() 的轨迹是抛物线.
的轨迹是抛物线.
焦点为![]() ,准线为
,准线为![]() .
.
所以曲线![]() 的方程为
的方程为![]() .
.
(2)由题意,过点![]() 的切线斜率存在,设切线方程为
的切线斜率存在,设切线方程为![]() ,
,
联立![]() 得
得![]() ,
,
所以![]() ,即
,即![]() (*),
(*),
因为![]() ,所以方程(*)存在两个不等实根,设为
,所以方程(*)存在两个不等实根,设为![]() ,
,
因为![]() ,所以
,所以![]() ,为定值.
,为定值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】函数f(x)=x2﹣x﹣2,x∈[﹣5,5],在定义域内任取一点x0 , 使f(x0)≤0的概率是( )
A.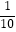
B.
C.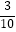
D.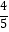
-
科目: 来源: 题型:
查看答案和解析>>【题目】在一次歌手大奖赛上,七位评委为歌手打出的分数如下:9.4,8.4,9.4,9.9,9.6,9.4,9.7,去掉一个最高分和一个最低分后,所剩数据的平均值和方差分别为( )
A.9.4,0.484
B.9.4,0.016
C.9.5,0.04
D.9.5,0.016 -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系
 中,已知动点
中,已知动点 到定点
到定点 的距离与到定直线
的距离与到定直线 的距离之比为
的距离之比为 .
.(1)求动点
 的轨迹
的轨迹 的方程;
的方程;(2)已知
 为定直线
为定直线 上一点.
上一点.①过点
 作
作 的垂线交轨迹
的垂线交轨迹 于点
于点 (
( 不在
不在 轴上),求证:直线
轴上),求证:直线 与
与 的斜率之积是定值;
的斜率之积是定值;②若点
 的坐标为
的坐标为 ,过点
,过点 作动直线
作动直线 交轨迹
交轨迹 于不同两点
于不同两点 ,线段
,线段 上的点
上的点 满足
满足 ,求证:点
,求证:点 恒在一条定直线上.
恒在一条定直线上. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知四边形ABCD是边长为1的正方形,PA⊥平面ABCD,N是PC的中点.
(Ⅰ)若PA=1,求二面角B﹣PC﹣D的大小;
(Ⅱ)求AN与平面PCD所成角的正弦值的最大值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某算法的流程图如图所示,运行相应程序,输出S的值是( )

A.60
B.61
C.62
D.63 -
科目: 来源: 题型:
查看答案和解析>>【题目】某市有大型超市200家、中型超市400家、小型超市1400 家.为掌握各类超市的营业情况,现按分层抽样方法抽取一个容量为100的样本,应抽取中型超市( )
A.70家
B.50家
C.20家
D.10家
相关试题

