【题目】如图,在直角坐标系![]() 中,圆
中,圆![]() 与
与![]() 轴负半轴交于点
轴负半轴交于点![]() ,过点
,过点![]() 的直线
的直线![]() ,
,![]() 分别与圆
分别与圆![]() 交于
交于![]() ,
,![]() 两点.
两点.

(1)若![]() ,
,![]() ,求△
,求△![]() 的面积;
的面积;
(2)过点![]() 作圆O的两条切线,切点分别为E,F,求
作圆O的两条切线,切点分别为E,F,求![]() ;
;
(3)若![]() ,求证:直线
,求证:直线![]() 过定点.
过定点.
参考答案:
【答案】(1)![]() ;(2)
;(2)![]() ;(3)见解析
;(3)见解析
【解析】
试题(1)直线AM的方程为![]() ,直线AN的方程为
,直线AN的方程为![]() ,由中位线定理知,
,由中位线定理知,![]() ,由此能求出
,由此能求出![]() 的面积.(2)由已知条件推导出
的面积.(2)由已知条件推导出![]() ,
,![]() ,由此能求出
,由此能求出![]() .(3)设直线
.(3)设直线![]() 的方程
的方程![]() ,则直线
,则直线![]() 的方程为
的方程为![]() ,联立方程
,联立方程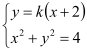 ,得
,得 同理
同理 ,由此能证明直线
,由此能证明直线![]() 过定点
过定点![]() .
.
试题解析:(1)由题知,得直线![]() 的方程为
的方程为![]() ,直线
,直线![]() 的方程为
的方程为![]()
所以,圆心到直线![]() 的距离
的距离![]() ,所以,
,所以,![]() ,由中位线定理知, AN=
,由中位线定理知, AN=![]() , 由题知
, 由题知![]() ,所以
,所以![]() ⊥
⊥![]() ,
,![]()
![]()
![]() =
=![]() .
.
(2)![]() ,
,![]() ,
,
所以![]() .
.
所以![]() ,
,
所以![]()
(3)由题知直线![]() 和直线
和直线![]() 的斜率都存在,且都不为0,不妨设直线
的斜率都存在,且都不为0,不妨设直线![]() 的的方程
的的方程![]() ,则直线
,则直线![]() 的方程为
的方程为![]() ,所以,联立方程
,所以,联立方程 ,所以,
,所以,![]() ,得
,得![]() 或
或![]() ,
,
所以![]() , 同理,
, 同理,![]() ,
,
因为![]() 轴上存在一点D
轴上存在一点D![]() ,
,
所以, =
=![]() ,同理
,同理![]() ,
,
所以,![]() =
=![]() ,所以,直线
,所以,直线![]() 过定点
过定点![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某篮球队对篮球运动员的篮球技能进行统计研究,针对篮球运动员在投篮命中时,运动员距篮筐中心的水平距离这项指标,对某运动员进行了若干场次的统计,依据统计结果绘制如下频率分布直方图:

(1)依据频率分布直方图估算该运动员投篮命中时,他到篮筐中心的水平距离的中位数;
(2)若从该运动员投篮命中时,他到篮筐中心的水平距离为2到5米的这三组中,用分层抽样的方法抽取7次成绩(单位:米,运动员投篮命中时,他到篮筐中心的水平距离越远越好),并从抽到的这7次成绩中随机抽取2次,并规定:成绩来自2到3米这一组时,记1分;成绩来自3到4米这一组时,记2分;成绩来4到5米的这一组记 4分,求该运动员2次总分不少于5分的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,网格纸上小正方形的边长为1,粗线画出的是某几何体的三视图,则它的体积为( )

A.48
B.16
C.32
D.16
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,三棱台
 中, 侧面
中, 侧面 与侧面
与侧面 是全等的梯形,若
是全等的梯形,若 ,且
,且 .
.
(Ⅰ)若
 ,
,  ,证明:
,证明:  ∥平面
∥平面 ;
;(Ⅱ)若二面角
 为
为 ,求平面
,求平面 与平面
与平面 所成的锐二面角的余弦值.
所成的锐二面角的余弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】设函数
 ,曲线
,曲线 在点
在点 处的切线方程为
处的切线方程为 .
.(1)求
 的解析式;
的解析式;(2)证明:曲线
 上任一点处的切线与直线
上任一点处的切线与直线 和直线
和直线 所围成的三角形面积为定值,并求此定值.
所围成的三角形面积为定值,并求此定值. -
科目: 来源: 题型:
查看答案和解析>>【题目】设定义在(0,+∞)上的函数f(x)满足xf′(x)﹣f(x)=xlnx,f(
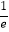 )=
)= 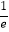 ,则f(x)( )
,则f(x)( )
A.有极大值,无极小值
B.有极小值,无极大值
C.既有极大值,又有极小值
D.既无极大值,也无极小值 -
科目: 来源: 题型:
查看答案和解析>>【题目】设数列{an}的前n项和为Sn , an是Sn和1的等差中项.
(1)求数列{an}的通项公式;
(2)求数列{nan}的前n项和Tn .
相关试题

