【题目】设数列{an}的前n项和为Sn , an是Sn和1的等差中项.
(1)求数列{an}的通项公式;
(2)求数列{nan}的前n项和Tn .
参考答案:
【答案】
(1)解:∵an是Sn和1的等差中项,
∴2an=Sn+1,2an﹣1=Sn﹣1+1(n≥2),
两式相减得:2an﹣2an﹣1=an,即an=2an﹣1,
又∵2a1=S1+1,即a1=1,
∴数列{an}是首项为1、公比为2的等比数列,
∴an=2n﹣1
(2)解:由(1)可知Tn=120+221+322+…+n2n﹣1,
2Tn=121+222+…+(n﹣1)2n﹣1+n2n,
两式相减得:﹣Tn=1+21+22+…+2n﹣1﹣n2n
= ![]() ﹣n2n
﹣n2n
=﹣1﹣(n﹣1)2n,
∴Tn=1+(n﹣1)2n
【解析】(1)通过等差中项的性质可知2an=Sn+1,并与2an﹣1=Sn﹣1+1(n≥2)作差,进而整理可知数列{an}是首项为1、公比为2的等比数列,计算即得结论;(2)通过(1)可知Tn=120+221+322+…+n2n﹣1 , 进而利用错位相减法计算即得结论.
【考点精析】通过灵活运用数列的前n项和和数列的通项公式,掌握数列{an}的前n项和sn与通项an的关系 ;如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式即可以解答此题.
;如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式即可以解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直角坐标系
 中,圆
中,圆 与
与 轴负半轴交于点
轴负半轴交于点 ,过点
,过点 的直线
的直线 ,
, 分别与圆
分别与圆 交于
交于 ,
, 两点.
两点.
(1)若
 ,
, ,求△
,求△ 的面积;
的面积;(2)过点
 作圆O的两条切线,切点分别为E,F,求
作圆O的两条切线,切点分别为E,F,求 ;
;(3)若
 ,求证:直线
,求证:直线 过定点.
过定点. -
科目: 来源: 题型:
查看答案和解析>>【题目】设函数
 ,曲线
,曲线 在点
在点 处的切线方程为
处的切线方程为 .
.(1)求
 的解析式;
的解析式;(2)证明:曲线
 上任一点处的切线与直线
上任一点处的切线与直线 和直线
和直线 所围成的三角形面积为定值,并求此定值.
所围成的三角形面积为定值,并求此定值. -
科目: 来源: 题型:
查看答案和解析>>【题目】设定义在(0,+∞)上的函数f(x)满足xf′(x)﹣f(x)=xlnx,f(
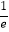 )=
)= 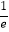 ,则f(x)( )
,则f(x)( )
A.有极大值,无极小值
B.有极小值,无极大值
C.既有极大值,又有极小值
D.既无极大值,也无极小值 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知梯形
 与梯形
与梯形 全等,
全等,  ,
,  ,
,  ,
,  ,
,  ,
,  为
为 中点.
中点. 
(Ⅰ)证明:
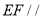 平面
平面
(Ⅱ)点
 在线段
在线段 上(端点除外),且
上(端点除外),且 与平面
与平面 所成角的正弦值为
所成角的正弦值为 ,求
,求 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,三棱锥P﹣ABC中,D是AC的中点,
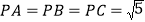 ,
,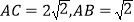 ,
,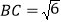 .
.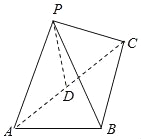
(1)求证:PD⊥平面ABC;
(2)求二面角P﹣AB﹣C的正切值大小.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某市在对学生的综合素质评价中,将其测评结果分为“优秀、合格、不合格”三个等级,其中不小于80分为“优秀”,小于60分为“不合格”,其它为“合格”. 参考公式:K2=
 ,其中n=a+b+c+d.
,其中n=a+b+c+d.
临界值表:P(K2≥k0)
0.15
0.10
0.05
0.025
0.010
k0
2.072
2.706
3.841
5.024
6.635
(1)某校高一年级有男生500人,女生400人,为了解性别对该综合素质评价结果的影响,采用分层抽样的方法从高一学生中抽取45名学生的综合素质评价结果,其各个等级的频数统计如下表:等级
优秀
合格
不合格
男生(人)
15
x
5
女生(人)
15
3
y
根据表中统计的数据填写下面2×2列联表,并判断是否有90%的把握认为“综合素质评价测评结果为优秀与性别有关”?
优秀
男生
女生
总计
非优秀
总计
(2)以(1)中抽取的45名学生的综合素质评价等级的频率作为全市各个评价等级发生的概率,且每名学生是否“优秀”相互独立,现从该市高一学生中随机抽取3人. ①求所选3人中恰有2人综合素质评价为“优秀”的概率;
②记X表示这3人中综合素质评价等级为“优秀”的个数,求X的数学期望.
相关试题

