【题目】甲、乙两企业生产同一种型号零件,按规定该型号零件的质量指标值落在![]() 内为优质品.从两个企业生产的零件中各随机抽出了500件,测量这些零件的质量指标值,得结果如下表:
内为优质品.从两个企业生产的零件中各随机抽出了500件,测量这些零件的质量指标值,得结果如下表:
甲企业:

乙企业:

(1)已知甲企业的500件零件质量指标值的样本方差![]() ,该企业生产的零件质量指标值
,该企业生产的零件质量指标值![]() 服从正态分布
服从正态分布![]() ,其中
,其中![]() 近似为质量指标值的样本平均数
近似为质量指标值的样本平均数![]() (注:求
(注:求![]() 时,同一组数据用该区间的中点值作代表),
时,同一组数据用该区间的中点值作代表),![]() 近似为样本方差
近似为样本方差![]() ,试根据该企业的抽样数据,估计所生产的零件中,质量指标值不低于71.92的产品的概率.(精确到0.001)
,试根据该企业的抽样数据,估计所生产的零件中,质量指标值不低于71.92的产品的概率.(精确到0.001)
(2)由以上统计数据完成下面![]() 列联表,并问能否在犯错误的概率不超过0.01的前提下,认为“两个分厂生产的零件的质量有差异”.
列联表,并问能否在犯错误的概率不超过0.01的前提下,认为“两个分厂生产的零件的质量有差异”.
附注:
参考数据: ![]() ,
,
参考公式: ![]() ,
, ![]() ,
,
![]() .
.
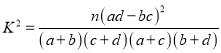
| 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
参考答案:
【答案】(1)0.159.(2)见解析.
【解析】试题分析:
(1)由题意求得![]() ,
, ![]() ,结合概率的性质可得甲企业零件质量指标值不低于71.92的产品的概率为0.159.
,结合概率的性质可得甲企业零件质量指标值不低于71.92的产品的概率为0.159.
(2)写出列联表,计算可得![]()
![]() 对照临界值表得出,在犯错的概率不超过0.01的前提下,认为“两个分厂生产的产品的质量有差异”.
对照临界值表得出,在犯错的概率不超过0.01的前提下,认为“两个分厂生产的产品的质量有差异”.
试题解析:
(1)依据上述数据,甲厂产品质量指标值的平均值为:
![]()
![]() ,
,
所以![]() ,
, ![]() ,
,
即甲企业生产的零件质量指标值![]() 服从正态分布
服从正态分布![]() ,
,
又![]() ,则,
,则,
![]()
![]() ,
,
![]()
![]() ,
,
所以,甲企业零件质量指标值不低于71.92的产品的概率为0.159.
(2)由以上统计数据填写![]() 列联表,如下:
列联表,如下:
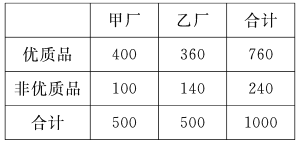
计算![]()
![]()
对照临界值表得出,在犯错的概率不超过0.01的前提下,认为“两个分厂生产的产品的质量有差异”.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
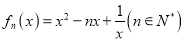 .
.(1)求曲线
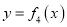 在点
在点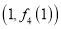 处的切线方程;
处的切线方程;(2)求函数
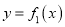 的极值;
的极值;(3)判断
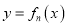 在
在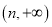 上的单调性,并加以说明.
上的单调性,并加以说明. -
科目: 来源: 题型:
查看答案和解析>>【题目】高二年级的一个研究性学习小组在网上查知,某珍贵植物种子在一定条件下发芽成功的概率为
 ,该研究性学习小组又分成两个小组进行验证性实验.
,该研究性学习小组又分成两个小组进行验证性实验.(1)第1组做了5次这种植物种子的发芽实验(每次均种下一粒种子),求他们的实验至少有3次成功的概率;
(2)第二小组做了若干次发芽试验(每次均种下一粒种子),如果在一次实验中种子发芽成功就停止实验,否则将继续进行下次实验,直到种子发芽成功为止,但发芽实验的次数最多不超过5次,求第二小组所做种子发芽实验的次数
 的概率分布列和期望.
的概率分布列和期望. -
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-4:坐标系与参数方程
在直角坐标系
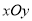 中,直线
中,直线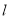 的参数方程是
的参数方程是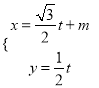 (
(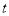 为参数).以坐标原点
为参数).以坐标原点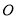 为极点,以
为极点,以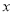 轴的正半轴为极轴,建立极坐标系,曲线
轴的正半轴为极轴,建立极坐标系,曲线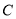 的极坐标方程是
的极坐标方程是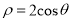 .
.(1)求直线
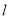 的普通方程和曲线
的普通方程和曲线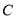 的直角坐标方程;
的直角坐标方程;(2)设点
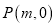 ,若直线
,若直线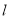 与曲线
与曲线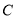 交于
交于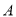 ,
, 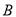 两点,且
两点,且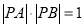 ,求实数
,求实数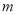 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在三棱锥
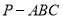 中,
中, 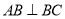 ,
, 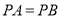 ,
, 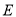 为
为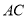 的中点.
的中点.(1)求证:
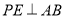 ;
;(2)设平面
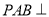 平面
平面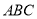 ,
, 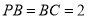 ,
, 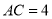 ,求二面角
,求二面角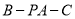 的平面角的正弦值.
的平面角的正弦值.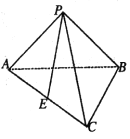
-
科目: 来源: 题型:
查看答案和解析>>【题目】某教师有相同的语文参考书3本,相同的数学参考书4本,从中取出4本赠送给4位学生,每位学生1本,则不同的赠送方法共有( )
A. 15种 B. 20种 C. 48种 D. 60种
-
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-5:不等式选讲
已知函数
 .
.(1)若
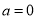 ,求不等式
,求不等式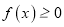 的解集;
的解集;(2)若方程
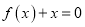 有三个不同的解,求实数
有三个不同的解,求实数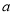 的取值范围.
的取值范围.
相关试题

