【题目】已知函数![]() .
.
(1)求曲线![]() 在点
在点![]() 处的切线方程;
处的切线方程;
(2)求函数![]() 的极值;
的极值;
(3)判断![]() 在
在![]() 上的单调性,并加以说明.
上的单调性,并加以说明.
参考答案:
【答案】(1)![]() .(2)见解析;(3)见解析
.(2)见解析;(3)见解析
【解析】试题分析 :(1)由题意可知![]() ,,
,, ![]() ,求出切点和斜率,由点斜式可求切线方程。(2)
,求出切点和斜率,由点斜式可求切线方程。(2)![]() ,
, ![]() ,定义域
,定义域![]() 导数等于0的根为1,据此可求出极值。(3)由(1)(2)可知
导数等于0的根为1,据此可求出极值。(3)由(1)(2)可知![]() ,
, ![]() 均满足在
均满足在![]()
上单调递增,所以如果有统计单调性的话,一定是单调递增,所以要证![]() 对
对![]() 恒成立。而
恒成立。而![]() 在
在![]() 上递增,
上递增, ![]() >0恒成立,即证。
>0恒成立,即证。
试题解析:(1)∵![]() ,∴
,∴![]() ,∴
,∴![]() ,∵
,∵![]() ,
,
∴曲线![]() 在点
在点![]() 处得切线方程为
处得切线方程为![]() ,即
,即![]() .
.
(2)∵![]() ,∴
,∴![]() ,
,
令![]() ,得
,得![]() ;令
;令![]() ,得
,得![]() 且
且![]() .
.
∴![]() 在
在![]() 上递增,在
上递增,在![]() 和
和![]() 上递减.
上递减.
故![]() 在
在![]() 处取得极小值,且极小值为
处取得极小值,且极小值为![]() ,
, ![]() 无极大值.
无极大值.
(3)![]() 在
在![]() 上递增.
上递增.
证明如下:
要证![]() 在
在![]() 上递增,
上递增,
只要证![]() 对
对![]() 恒成立,
恒成立,
即证![]() 对
对![]() 恒成立.
恒成立.
∵![]() 在
在![]() 上递增,∴
上递增,∴![]() .
.
故要证![]() 对
对![]() 恒成立,
恒成立,
只要证![]() 对
对![]() 恒成立,
恒成立,
即证![]() 对
对![]() 恒成立,即证
恒成立,即证![]() 对
对![]() 恒成立,
恒成立,
∵![]() ,∴
,∴![]() ,∴
,∴![]() 对
对![]() 恒成立,
恒成立,
故![]() 在
在![]() 上递增.
上递增.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在心理学研究中,常采用对比试验的方法评价不同心理暗示对人的影响,具体方法如下:将参加试验的志愿者随机分成两组,一组接受甲种心理暗示,另一组接受乙种心理暗示,通过对比这两组志愿者接受心理暗示后的结果来评价两种心理暗示的作用,现有5名男志愿
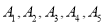 和3名女志愿者
和3名女志愿者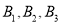 ,从中随机抽取4人接受甲种心理暗示,另4人接受乙种心理暗示.
,从中随机抽取4人接受甲种心理暗示,另4人接受乙种心理暗示. (1)求接受甲种心理暗示的志愿者中包含
 但不包含
但不包含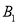 的频率.
的频率. (2)用
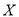 表示接受乙种心理暗示的女志愿者人数,求
表示接受乙种心理暗示的女志愿者人数,求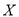 的分布列与数学期望
的分布列与数学期望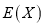
-
科目: 来源: 题型:
查看答案和解析>>【题目】为美化小区环境,某社区针对公民乱扔垃圾的现象进行了罚款处罚,并随机抽取了200人进行调查,得到如下数据:

(1)若乱扔垃圾的人数
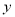 与罚款金额
与罚款金额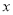 (单位:元)满足线性回归关系,求回归方程;
(单位:元)满足线性回归关系,求回归方程;(2)由(1)得到的回归方程分析要使乱扔垃圾的人数不超过
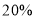 ,罚款金额至少是多少元?
,罚款金额至少是多少元?参考公式:两个具有线性关系的变量的一组数据:
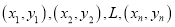 ,
,其回归方程为
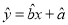 ,其中
,其中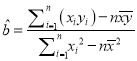 ,
, 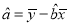
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了调查某高中学生每天的睡眠时间,随即对20名男生和20名女生进行问卷调查.
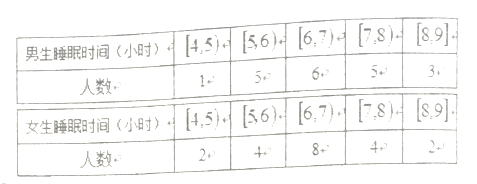
(1)现把睡眠时间不足5小时的定义为“严重睡眠不足”,从睡眠时间不足6小时的女生中随机抽取3人,求此3人中恰有一人为“睡眠严重不足”的概率;
(2)完成下面
 列联表,并回答是否有
列联表,并回答是否有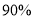 的把握认为“睡眠时间与性别有关”?
的把握认为“睡眠时间与性别有关”?
参考公式:
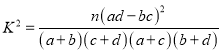 ,
, 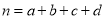
临界表值:

-
科目: 来源: 题型:
查看答案和解析>>【题目】高二年级的一个研究性学习小组在网上查知,某珍贵植物种子在一定条件下发芽成功的概率为
 ,该研究性学习小组又分成两个小组进行验证性实验.
,该研究性学习小组又分成两个小组进行验证性实验.(1)第1组做了5次这种植物种子的发芽实验(每次均种下一粒种子),求他们的实验至少有3次成功的概率;
(2)第二小组做了若干次发芽试验(每次均种下一粒种子),如果在一次实验中种子发芽成功就停止实验,否则将继续进行下次实验,直到种子发芽成功为止,但发芽实验的次数最多不超过5次,求第二小组所做种子发芽实验的次数
 的概率分布列和期望.
的概率分布列和期望. -
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-4:坐标系与参数方程
在直角坐标系
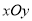 中,直线
中,直线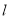 的参数方程是
的参数方程是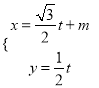 (
(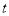 为参数).以坐标原点
为参数).以坐标原点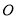 为极点,以
为极点,以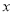 轴的正半轴为极轴,建立极坐标系,曲线
轴的正半轴为极轴,建立极坐标系,曲线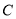 的极坐标方程是
的极坐标方程是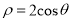 .
.(1)求直线
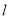 的普通方程和曲线
的普通方程和曲线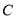 的直角坐标方程;
的直角坐标方程;(2)设点
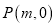 ,若直线
,若直线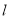 与曲线
与曲线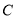 交于
交于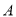 ,
, 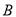 两点,且
两点,且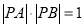 ,求实数
,求实数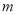 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两企业生产同一种型号零件,按规定该型号零件的质量指标值落在
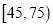 内为优质品.从两个企业生产的零件中各随机抽出了500件,测量这些零件的质量指标值,得结果如下表:
内为优质品.从两个企业生产的零件中各随机抽出了500件,测量这些零件的质量指标值,得结果如下表:甲企业:

乙企业:

(1)已知甲企业的500件零件质量指标值的样本方差
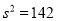 ,该企业生产的零件质量指标值
,该企业生产的零件质量指标值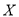 服从正态分布
服从正态分布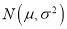 ,其中
,其中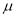 近似为质量指标值的样本平均数
近似为质量指标值的样本平均数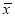 (注:求
(注:求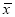 时,同一组数据用该区间的中点值作代表),
时,同一组数据用该区间的中点值作代表),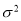 近似为样本方差
近似为样本方差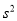 ,试根据该企业的抽样数据,估计所生产的零件中,质量指标值不低于71.92的产品的概率.(精确到0.001)
,试根据该企业的抽样数据,估计所生产的零件中,质量指标值不低于71.92的产品的概率.(精确到0.001)(2)由以上统计数据完成下面
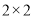 列联表,并问能否在犯错误的概率不超过0.01的前提下,认为“两个分厂生产的零件的质量有差异”.
列联表,并问能否在犯错误的概率不超过0.01的前提下,认为“两个分厂生产的零件的质量有差异”.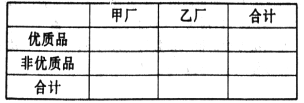
附注:
参考数据:
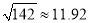 ,
,参考公式:
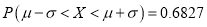 ,
, 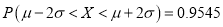 ,
,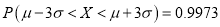 .
.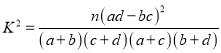
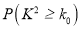
0.50
0.40
0.25
0.15
0.10
0.05
0.025
0.010
0.005
0.001

0.455
0.708
1.323
2.072
2.706
3.841
5.024
6.635
7.879
10.828
相关试题

